The average final exam score for the statistics course is 74%. A professor wants to see if the average final exam score for students who are given colored pens on the first day of class is higher. The final exam scores for the 16 randomly selected students who were given the colored pens are shown below. Assume that the distribution of the population is normal. 85, 71, 89, 88, 62, 71, 94, 82, 67, 70, 98, 88, 80, 88, 92, 65 What can be concluded at the the a = 0.10 level of significance level of significance? a. For this study, we should use Select an answer b. The null and alternative hypotheses would be: Ho: ? ? Hị: ? c. The test statistic ? O (please show your answer to 3 decimal places.) %3D d. The p-value : e. The p-value is ? O a (Please show your answer to 4 decimal places.) f. Based on this, we shoul v Select an answer the null hypothesis. аcсept g. Thus, the final conclusi reject fail to reject OThe data suggest lean final exam score for students who are given colored pens at the beginning of class is not significantly higher than 74 at a = 0.10, so there is statistically insignificant evidence to conclude that the population mean final exam score for students who are given colored pens at the beginning of class is higher than 74. The data suggest the population mean is not significantly higher than 74 at a = 0.10, so there is statistically insignificant evidence to conclude that the population mean final exam score for students who are given colored pens at the beginning of class is equal to 74. OThe data suggest the populaton mean is significantly higher than 74 at a = 0.10, so there is statistically significant evidence to conclude that the population mean final exam score for students who are given colored pens at the beginning of class is higher than 74.
The average final exam score for the statistics course is 74%. A professor wants to see if the average final exam score for students who are given colored pens on the first day of class is higher. The final exam scores for the 16 randomly selected students who were given the colored pens are shown below. Assume that the distribution of the population is normal. 85, 71, 89, 88, 62, 71, 94, 82, 67, 70, 98, 88, 80, 88, 92, 65 What can be concluded at the the a = 0.10 level of significance level of significance? a. For this study, we should use Select an answer b. The null and alternative hypotheses would be: Ho: ? ? Hị: ? c. The test statistic ? O (please show your answer to 3 decimal places.) %3D d. The p-value : e. The p-value is ? O a (Please show your answer to 4 decimal places.) f. Based on this, we shoul v Select an answer the null hypothesis. аcсept g. Thus, the final conclusi reject fail to reject OThe data suggest lean final exam score for students who are given colored pens at the beginning of class is not significantly higher than 74 at a = 0.10, so there is statistically insignificant evidence to conclude that the population mean final exam score for students who are given colored pens at the beginning of class is higher than 74. The data suggest the population mean is not significantly higher than 74 at a = 0.10, so there is statistically insignificant evidence to conclude that the population mean final exam score for students who are given colored pens at the beginning of class is equal to 74. OThe data suggest the populaton mean is significantly higher than 74 at a = 0.10, so there is statistically significant evidence to conclude that the population mean final exam score for students who are given colored pens at the beginning of class is higher than 74.
MATLAB: An Introduction with Applications
6th Edition
ISBN:9781119256830
Author:Amos Gilat
Publisher:Amos Gilat
Chapter1: Starting With Matlab
Section: Chapter Questions
Problem 1P
Related questions
Concept explainers
Addition Rule of Probability
It simply refers to the likelihood of an event taking place whenever the occurrence of an event is uncertain. The probability of a single event can be calculated by dividing the number of successful trials of that event by the total number of trials.
Expected Value
When a large number of trials are performed for any random variable ‘X’, the predicted result is most likely the mean of all the outcomes for the random variable and it is known as expected value also known as expectation. The expected value, also known as the expectation, is denoted by: E(X).
Probability Distributions
Understanding probability is necessary to know the probability distributions. In statistics, probability is how the uncertainty of an event is measured. This event can be anything. The most common examples include tossing a coin, rolling a die, or choosing a card. Each of these events has multiple possibilities. Every such possibility is measured with the help of probability. To be more precise, the probability is used for calculating the occurrence of events that may or may not happen. Probability does not give sure results. Unless the probability of any event is 1, the different outcomes may or may not happen in real life, regardless of how less or how more their probability is.
Basic Probability
The simple definition of probability it is a chance of the occurrence of an event. It is defined in numerical form and the probability value is between 0 to 1. The probability value 0 indicates that there is no chance of that event occurring and the probability value 1 indicates that the event will occur. Sum of the probability value must be 1. The probability value is never a negative number. If it happens, then recheck the calculation.
Topic Video
Question
need help with B, C, D
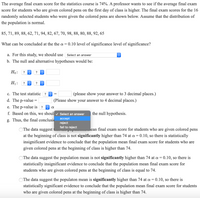
Transcribed Image Text:**Educational Website Text: Statistical Analysis of Exam Scores**
**Context:**
The purpose of this study is to assess whether providing colored pens to students on the first day of class influences their final exam scores in a statistics course. The course's average final score is known to be 74%, and a professor aims to determine if the average score increases with the provision of colored pens. Here are the scores for 16 students who received colored pens:
**Scores:**
85, 71, 89, 88, 62, 71, 94, 82, 67, 70, 98, 88, 80, 88, 92, 65
**Statistical Analysis:**
**Objective:**
To evaluate at a significance level (\(\alpha = 0.10\)), whether the average final score for students who received colored pens is significantly higher than 74.
**Steps:**
- **a. Level of Significance:**
For this study, select the correct level of significance.
- **b. Hypotheses:**
- \(H_0\): (Null Hypothesis) The mean score is equal to 74.
- \(H_1\): (Alternative Hypothesis) The mean score is greater than 74.
- **c. Test Statistic:**
Calculate and enter the test statistic to three decimal places.
- **d. P-value:**
Determine and provide the p-value to four decimal places.
- **e. P-value vs. \(\alpha\):**
Compare the p-value with \(\alpha = 0.10\).
- **f. Decision on Null Hypothesis:**
Based on the above, decide to accept or reject the null hypothesis.
- **g. Conclusion:**
Use the findings to conclude:
- Option 1: The data suggest that the population mean final exam score for students who use colored pens is not significantly higher than 74.
- Option 2: The data suggest the population mean is not significantly higher than 74; hence, no evidence supports a higher mean.
- Option 3: The data suggest the population mean is significantly higher than 74, supporting the effectiveness of colored pens.
This analysis helps evaluate the potential impact of colored pens on student performance, based on statistical evidence.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 2 steps with 1 images
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Recommended textbooks for you
MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc
Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning
Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning
MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc
Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning
Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning
Elementary Statistics: Picturing the World (7th E…
Statistics
ISBN:
9780134683416
Author:
Ron Larson, Betsy Farber
Publisher:
PEARSON
The Basic Practice of Statistics
Statistics
ISBN:
9781319042578
Author:
David S. Moore, William I. Notz, Michael A. Fligner
Publisher:
W. H. Freeman
Introduction to the Practice of Statistics
Statistics
ISBN:
9781319013387
Author:
David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:
W. H. Freeman