
College Physics
11th Edition
ISBN: 9781305952300
Author: Raymond A. Serway, Chris Vuille
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Question
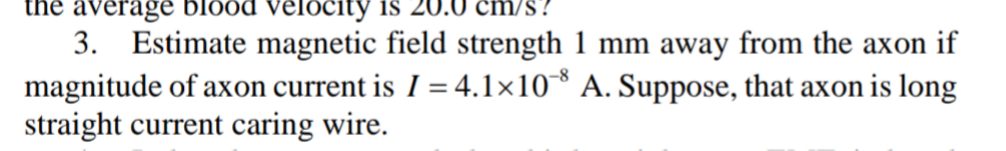
Transcribed Image Text:the average
blood velocity is 20.0 cm/s?
3. Estimate magnetic field strength 1 mm away from the axon if
magnitude of axon current is I = 4.1×10 A. Suppose, that axon is long
straight current caring wire.

Transcribed Image Text:Magnetism.pdf
MAGNETIC FIELD. MAGNETISM IN NATURE
1. The magnitude of the magnetic force F on a charge q moving at a speed v in a magnetic field of
strength B is given by F = qvBsin0, where 0 is the angle between the directions of v and B. This force is
often called the Lorentz force. In fact, this is how we define the magnetic field strength B in terms of the
force on a charged particle moving in a magnetic field. The SI unit for magnetic field strength B is called the
tesla (T).
2. Force on a moving charge in a magnetic field. Magnetic force can cause a charged particle to move
in a circular or spiral path. In this case, the magnetic force supplies the centripetal force.
mv?
= qvB, here, r is the radius of curvature of the path of a charged particle with mass m and charge q ,
moving at a speed v perpendicular to a magnetic field of strength B (0 = 1) .
3. The Hall Effect
The magnetic field also affects charges moving in a
conductor. Figure 1 shows what happens to charges moving
OB (out of paper)
RHR-1
F.
through a conductor in a magnetic field. The field is
perpendicular to the electron drift velocity and to the width
(a) i O
of the conductor. Note that conventional current is to the
right in both parts of the figure. In part (a), electrons carry
the current and move to the left. In part (b), positive charges
carry the current and move to the right. Moving electrons
feel a magnetic force toward one side of the conductor,
leaving a net positive charge on the other side. This
separation of charge creates a voltage ɛ , known as the Hall
emf, across the conductor. The creation of a voltage across a current-carrying conductor by a magnetic field
в
(b) -E O
F.
is known as the Hall effect: qE = qvB, or E = vB.
Note that the electric field E is uniform across the conductor because the magnetic field B is uniform, as is
the conductor. For a uniform electric field, the relationship between electric field and voltage is E = ɛ/l ,
where l is the width of the conductor and ɛ is the Hall EMF. Entering this into the last expression gives
ɛ = Blv
where ɛ is the Hall effect voltage across a conductor of width I through which charges move at a speed v.
The Hall effect can be used to measure fluid flow in any fluid having free charges, such as blood.
4. Magnetic force on a current-carrying conductor F = IlBsin0, here F is magnetic force on a length
1 of wire carrying a current I in a uniform magnetic field B.
5. The torque t on a current-carrying loop of any shape in a uniform magnetic field is t = NIABsin0,
where N is the number of turns, I is the current, A is the area of the loop, B is the magnetic field strength, and
O is the angle between the perpendicular to the loop and the magnetic field.
6. The magnetic field strength (magnitude) produced by a long straight current-carrying wire is
found by experiment to be B = 20, where I is the current, r is the shortest distance to the wire, and the
constant uo = 4x×10¯7 T · m/A is the permeability of free space.
7. Magnetic field produced by a current-carrying circular loop. There is a simple formula for the
magnetic field strength at the center of a circular loop. It is B =, where R is the radius of the loop. One
2πr'
Нol
2R
way to get a larger field is to have N loops; then, the field is B = N Ho!.
2R
Holil2
, here two parallel currents I1 and I2,
8. Magnetic force between two parallel conductors
%3D
2nr
separated by a distance r, l is length of the conductors.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 2 images

Knowledge Booster
Similar questions
- Describe the physical quantity electrical resistance of a wire made from a given material, length L, and cross-sectional area A.arrow_forwardCheck Score A current of 4.50 A flows in a conductor for 9.50 s. How many electrons pass a given point in the conductor during this time? 0.47 X electrons Hide Answer Try Another Need Help? Read It Show My Work (Optional)? Submit Answer F1 F2 20 F3 $ F4 Question 1 of 7 View Next Question % k F5 MacBook Air F6 & r F7 DII * 00 FBarrow_forwardneed help with followingarrow_forward
- A 1 XXX XX X X X X X XXXXX F=2x104 Downward b= 8MC force * find magnitude and direction of the speed of charge "mignatic feild Pointing to the right* B=2x10" T L=1m 2 *Acharge in a mignatic feild going into the page. *4 B = 2x10-³+ V=? Cuine Current I= 2s find the Direction of the force 3 magnitudo acting on this wire goiry Downarrow_forwardA heart defibrillator used by emergency medical sta to restart an accident victim’s heart has a power supply that produces an average 5000V over a short period of time. A defibrillator is basically a capacitor that discharges its stored charge in such a way that the charge moves through the human body, across the heart, as a current. If this capacitor is created from charging up plates 5cm on each side, with plastic insulator spacing of 3cm between the plates, then how much charge did the plates transfer to the human body?arrow_forwardIf the voltage is 100 volts, what is the current through R2?arrow_forward
- Opening of voltage-gated channels is driven by an intramembrane electric field acting on charged voltage-sensor domains. These domains move across the membrane and generate gating (displacement) currents. When these currents are integrated over time, they produce the gating charge generated by a population of channels. What would be the gating charge passing through the external circuit when the flat array of charges moves across the distance a inside the membrane? The hydrophobic thickness of the membrane is d, the dielectric constant ɛ, the density of charges is O and the area of the membrane is A (provide an analytic solution). start end A A a d darrow_forwardA myelinated axon conducts nerve impulses at a speed of 40 m/s. What is the signal speed if the thickness of the myelin sheath is halved but no other changes are made to the axon?arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON

College Physics
Physics
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning

University Physics (14th Edition)
Physics
ISBN:9780133969290
Author:Hugh D. Young, Roger A. Freedman
Publisher:PEARSON

Introduction To Quantum Mechanics
Physics
ISBN:9781107189638
Author:Griffiths, David J., Schroeter, Darrell F.
Publisher:Cambridge University Press

Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning

Lecture- Tutorials for Introductory Astronomy
Physics
ISBN:9780321820464
Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina Brissenden
Publisher:Addison-Wesley

College Physics: A Strategic Approach (4th Editio...
Physics
ISBN:9780134609034
Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart Field
Publisher:PEARSON