
MATLAB: An Introduction with Applications
6th Edition
ISBN: 9781119256830
Author: Amos Gilat
Publisher: John Wiley & Sons Inc
expand_more
expand_more
format_list_bulleted
Question
Please solve the following attached question and round as needed in parts a and b.
In part b, options for H0 and H1 null and alternatives hypotheses are:
There is no lack of fit for the model
A linear model would fit the data better than a quadratic model
A cubic model would fit the data better than a quadratic model
An exponential model would fit the data better than a quadratic model
There is a lack of fit for the model
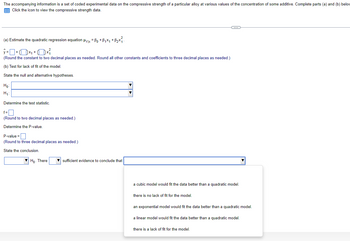
Transcribed Image Text:The accompanying information is a set of coded experimental data on the compressive strength of a particular alloy at various values of the concentration of some additive. Complete parts (a) and (b) below
Click the icon to view the compressive strength data.
(a) Estimate the quadratic regression equation μyx = ßo +ß₁×₁ +ß₂ײ.
(Round the constant to two decimal places as needed. Round all other constants and coefficients to three decimal places as needed.)
(b) Test for lack of fit of the model.
State the null and alternative hypotheses.
Ho
H₁
Determine the test statistic.
f=
(Round to two decimal places as needed.)
Determine the P-value.
P-value=
(Round to three decimal places as needed.)
State the conclusion.
Ho. There
sufficient evidence to conclude that
a cubic model would fit the data better than a quadratic model.
there is no lack of fit for the model.
an exponential model would fit the data better than a quadratic model.
a linear model would fit the data better than a quadratic model.
there is a lack of fit for the model.
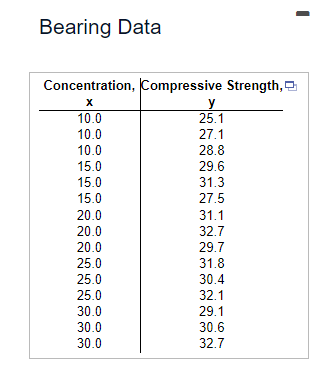
Transcribed Image Text:Bearing Data
Concentration, Compressive Strength,
x
y
10.0
25.1
10.0
27.1
10.0
28.8
15.0
29.6
15.0
31.3
15.0
27.5
20.0
31.1
20.0
32.7
20.0
29.7
25.0
31.8
25.0
30.4
25.0
32.1
30.0
29.1
30.0
30.6
30.0
32.7
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps

Knowledge Booster
Similar questions
- Read through this scenario and look at the data that was collected. State the null and all possible research hypotheses. Review the results below (I used SPSS) and answer the questions that follow. Scenario: A researcher wants to see if gender and / or income affects the total amount of help given to a stranger who is sitting on the side of a busy road with a sign asking for help. The independent variables are gender, income, and the interaction of gender and income. The dependent variable is total help. He wants to know if one or both factors – or the interaction of the two - affects the total amount of help offered. Because he is analyzing two independent variables (gender and income), he used a factorial ANOVA. His results show the main effect of each of the independent variables on the dependent variable (total help) and the interaction effect. The researcher is using a 95% confidence interval which means that he wants to be at least 95% sure that his independent variables…arrow_forwardhelp please answer in text form with proper workings and explanation for each and every part and steps with concept and introduction no AI no copy paste remember answer must be in proper format with all workingarrow_forwardMany questions in research can be expressed as two competing statements about the population parameter. These two statements are called the null and the alternative hypotheses. Usually, the researcher hopes the sample evidence will be in favor of the alternative hypothesis, the new theory. It is important to be able to state the theories that are being put to a test. Write out the hypotheses to be put to the test and define the parameter of interest in context of the problem. Do a minority of Michigan residents clear snow from sidewalks before 9 am after snow has fallen?For this scenario, write out the hypotheses to be put to the test and define the parameter of interest in context of the problem. H0:Ha: The parameter p represents ___(provide appropriate definition in context)________arrow_forward
- Which of the following is a thesis statement? (Check all that apply.) Note this question isn't about which statement is correct but which statement is a thesis statement. Smaller states have a more efficient government, holding education levels constant. Higher levels of income decrease murder rates. Why does is a country's median age correlated with its citizens' average wealth? This paper explores some causes of poverty.arrow_forwardPlease calculate the following Chi Square equations. 2. Chi Square Two Sample An agency director would like to determine whether there is a significant differences between participants in a group treatment verses individual treatment program for reducing cigarette smoking. Conduct a Chi-square test of independence to answer this question. Use the hypothesis steps provided in the lecture videos determine whether there is a significant difference between treatment group outcomes. State whether you reject or fail to reject the null hypothesis.arrow_forwardA social psychologist wants to see if altruism is significantly related to a person’s general health. He gets altruism scores and a measure of general health from the participants’ medical providers. The data are listed below. Higher altruism scores mean greater altruism, while high health scores = good health. Complete the appropriate statistical test and hypothesis testing using the 4 step approac Participant altruism X health Y X squared Y squared (X)(Y) A 101 33 3333 B 93 40 3720 C 85 24 2040 D 111 46 5106 E 104 30 3120 F 89 28 2492 Total State your conclusion in APA format. Alpha level = .05.arrow_forward
- You may need to use the appropriate appendix table or technology to answer this question. A national standardized test consists of three parts: critical reading, mathematics, and writing. Suppose each part of the test is scored on a 200- to 800-point scale with a median of approximately 510. Scores for each part of the test can be assumed to be symmetric. Use the following data to test the hypothesis that the population median score for the students taking the writing portion of the test is 510. 635 701 439 447 464 502 405 453 471 476 447 590 337 387 514 State the null and alternative hypotheses. O Ho: Median # 510 H₂: Median = 510 O Ho: Median 2 510 H₂: Median 510 ✓ Find the value of the test statistic. T = Find the p-value. (Round your answer to four decimal places.) p-value = Using a = 0.05, what is your conclusion? O Reject Ho. There is sufficient evidence to conclude that the population median writing test score is not 510. Ⓒ Do not reject Ho. There is not sufficient evidence to…arrow_forwardOnly answer 4 and 5, thank you Use the SPSS information on the following pages to complete your analysis and paper. Respond to the following in your paper. 1. The two variables for this study are age and consumer sense of entitlement. Which one is the independent variable? Which one is the dependent variable? 2. What are the null hypothesis and the alternate hypothesis for this study? 3. What is the R2 for this study? What does the R2 value mean? Be specific to this study in your explanation of the meaning of the R2 value. 4. What is the regression equation for this study? 5. What is the finding for this study, using a significance level of p < .10? What implications does this finding have on marketing? SPSS Regression Variables Entered/Removeda Model Variables Entered Variables Removed Method 1 Ageb . Enter a. Dependent Variable: Entitlement b. All requested variables entered. Model Summary Model R R Square Adjusted R…arrow_forwardIn 2020, the Lakers beat the Heat in the NBA championship. Beth is a Lakers fan. Alex is Heat fan. Even though the Lakers won the championship, they need to know once and for all: which team had the better players during the regular season in 2020? Write up your results as you would see it in a results section of an empirical research paper (in APA style). Make sure to include the means and SDs.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman

MATLAB: An Introduction with Applications
Statistics
ISBN:9781119256830
Author:Amos Gilat
Publisher:John Wiley & Sons Inc

Probability and Statistics for Engineering and th...
Statistics
ISBN:9781305251809
Author:Jay L. Devore
Publisher:Cengage Learning

Statistics for The Behavioral Sciences (MindTap C...
Statistics
ISBN:9781305504912
Author:Frederick J Gravetter, Larry B. Wallnau
Publisher:Cengage Learning

Elementary Statistics: Picturing the World (7th E...
Statistics
ISBN:9780134683416
Author:Ron Larson, Betsy Farber
Publisher:PEARSON

The Basic Practice of Statistics
Statistics
ISBN:9781319042578
Author:David S. Moore, William I. Notz, Michael A. Fligner
Publisher:W. H. Freeman

Introduction to the Practice of Statistics
Statistics
ISBN:9781319013387
Author:David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:W. H. Freeman