
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Concept explainers
Topic Video
Question
help

Transcribed Image Text:**Task 1. Building f(x) = sin(x)**
Using the Unit Circle that we built before, put the values of sin(x) for each angle below. Then see each point plotted in the graph. Compare the behavior of the graph with your answer about the change in y-coordinate from the Warm Up.
**Graph Explanation:**
The graph on the left has the y-axis labeled as "sin(x)" ranging from -2 to 2. The x-axis is labeled as "x (degrees)" ranging from 0 to 360 degrees, marked in increments of 30 degrees. You will plot the sine values for each corresponding angle from the table provided.
**Table:**
| x (degrees) | Sin(x) |
|-------------|------------------|
| 0 | |
| 30 | |
| 45 | |
| 60 | |
| 90 | |
| 120 | |
| 135 | |
| 150 | |
| 180 | |
| 210 | |
| 225 | |
| 240 | |
| 270 | |
| 300 | |
| 315 | |
| 330 | |
| 360 | |
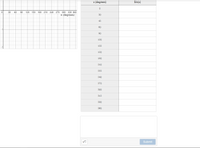
Transcribed Image Text:**Educational Website Content: Understanding the Sine Function**
**Introduction:**
The sine function, represented as sin(x), is fundamental in trigonometry and has applications in various fields such as physics, engineering, and computer science. It describes a smooth, periodic oscillation.
**Graph Explanation:**
The image displays a graph and a table related to the sine function.
1. **Graph:**
- The graph on the left shows the sine function plotted against angles ranging from 0 to 360 degrees.
- The x-axis represents the angle in degrees.
- The y-axis, ranging from -2 to 2, represents the sine values.
- The sine curve is periodic and oscillates between -1 and 1.
2. **Table:**
- The table on the right is meant to record the values of sin(x) for various angles x.
- The first column lists angle values in degrees: 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, 330°, 360°
- The second column is for the corresponding sine values to be filled in for each angle.
**Data Entry:**
To complete the table:
- Use the sine function on a calculator or mathematical software to find the sine values for the given angles.
- For example:
- Sin(0°) = 0
- Sin(30°) = 0.5
- Sin(45°) = √2/2 ≈ 0.707
- Continue this process for all listed angles.
**Interactive Component:**
- An input box labeled "Submit" is provided below the table for entering and submitting the calculated sine values.
**Conclusion:**
Understanding the sine function and its values for different angles is crucial for further studies in trigonometry and its applications. Once you've filled in the table, you'll have a clearer picture of how the sine function behaves.
**Note:** Errors in sine value calculation can lead to misunderstandings in subsequent applications, so double-check your values for accuracy.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 3 steps with 4 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

