
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
Prove the domination laws in Table 1 by showing that
a) A ∪ U = U. b) A ∩ ∅ = ∅.
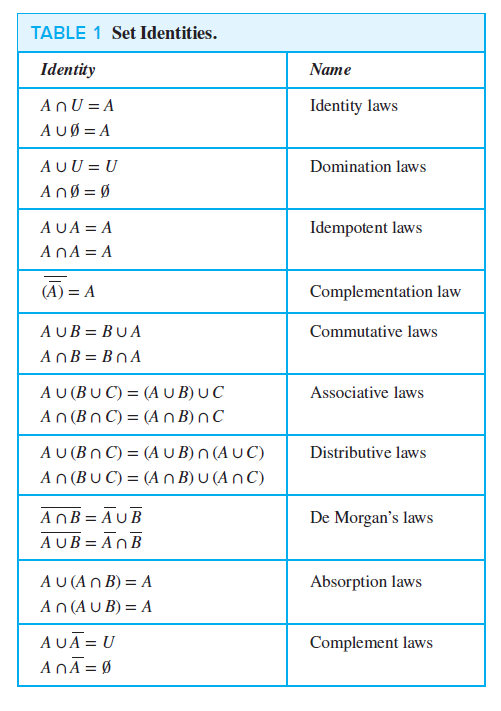
Transcribed Image Text:TABLE 1 Set Identities.
Identity
Name
AnU = A
Identity laws
AUØ = A
AUU = U
AnØ = Ø
Domination laws
AUA = A
AnA = A
Idempotent laws
(A) = A
Complementation law
AUB = BUA
Commutative laws
AnB = BOA
AU (BU C) = (A U B) U C
An (Bn C) = (A n B)nC
Associative laws
AU (Bn C) = (A U B) n (A U C)
An (BU C) = (A n B) U (An C)
Distributive laws
AOB = AUB
AUB = AnB
De Morgan's laws
AU (An B) = A
Absorption laws
An (AU B) = A
AUĀ = U
A NĀ= Ø
Complement laws
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- Question 9 f) Let A, B and C be sets. Prove that A ⊆ C and B ⊆ C, then A ∪ B ⊆ Carrow_forwardShow that if A and B are sets, then a) A – B = A n B. b) (An B) U (A O B) = A.arrow_forward1. Is the following axiom system of a consistent/dependent? a. There are six points. b. There are three 3-point lines. c. There are at least three 2-point lines. near-linear spacearrow_forward
- 2. Consider the function y(x) = 5x over the interval [0, 10]. (a) If the points A(0, y(0)), B(5, y(5)), and C(10, y(10)) are on the curve represented by the above function, find the slope of the lines (secants) AB, and AC, respectively. (b) If x represents time and y represents the displacement of a particle moving along a line, what is the physical meaning of your results to part (a)? (c) Now consider a point D(10 – h, y(10 – h)) on the curve represented by the given function, find the slope of the line DC. (d) As h → 0, what is the limiting value of your result to part (c)? (e) What is its physical meaning of your result to part (d) if again x represents time and y represents the displacement?arrow_forwardThis Venn diagram represents areas for students who like different subjects in all combinations List all areas (in an ascending order) that represent students who like the following:(For example for students who like History you need to put 4,5,6,7 No spaces between symbols.) a) like Math only b) like English and History c) Do not like Math d) Like Math or History e) Like English and History, but do not like Math f) Like Math or English, but do not like Historyarrow_forward21. Show that if A and B are sets, then a) AB=An B. b) (An B) U (An B) = A.arrow_forward
- Show that:a) Every element of A belongs to some equivalence class.b) Two elements are equivalent if and only if their equivalence classes are equalc) Two equivalence classes are either identical or they are disjoint.arrow_forward5) Suppose a path C is defined by r(t), 2 and r(8)= . If f is a differentiable function satisfying f(3,9) = 6 and f(6, 10) = 14, what is the value of Vf dr?arrow_forwardSuppose set A = {green, blue, red} and set B = {gray, purple, blue} (a) What is A ∪ B? (b) What is A ∩ B?arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

