Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Related questions
Question
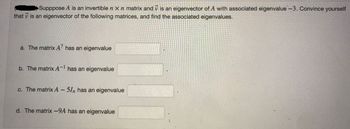
Transcribed Image Text:Supppose A is an invertible n x n matrix and is an eigenvector of A with associated eigenvalue -3. Convince yourself
that is an eigenvector of the following matrices, and find the associated eigenvalues.
a. The matrix A7 has an eigenvalue
b. The matrix A-1 has an eigenvalue
c. The matrix A - 57n has an eigenvalue
d. The matrix -9A has an eigenvalue
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 3 images
Knowledge Booster
Similar questions
- Supppose A is an invertible n x n matrix and v is an eigenvector of A with associated eigenvalue -4. Convince yourself that vis an eigenvector of the following matrices, and find the associated eigenvalues. a. The matrix A7 has an eigenvalue b. The matrix A-1 has an eigenvalue c. The matrix A + 51, has an eigenvalue d. The matrix -9A has an eigenvaluearrow_forwardSupppose A is an invertible n x n matrix and 7 is an eigenvector of A with associated eigenvalue 7. Convince yourself that is an eigenvector of the following matrices, and find the associated eigenvalues. a. The matrix A6 has an eigenvalue b. The matrix A¹ has an eigenvalue c. The matrix A + 8I, has an eigenvalue d. The matrix -6A has an eigenvaluearrow_forwardFind the eigenvalues of the symmetric matrix. (Enter your answers as a comma-separated list. Enter your answers from smallest to largest 0 55 5 0 5 5 5 5 A; = For each eigenvalue, find the dimension of the corresponding eigenspace. (Enter your answers as a comma-separated list.) dim(x;) =arrow_forward
- . Find all eigenvalues of the matrix vector for each eigenvalue. -16 8 -40 20 and an (explicit) eigen- . Verify that the Cayley-Hamilton Theorem holds for the matrix A = -16 8 -40 20arrow_forwardFor the matrix A, find (if possible) a nonsingular matrix P such that PAP is diagonal. (If not possible, enter IMPOSSIBLE.) 2 -2 5 A = 3 -2 L0 -1 2 P = Verify that PAP is a diagonal matrix with the eigenvalues on the main diagonal. p-1AP =arrow_forwardFind the eigenvalues of the symmetric matrix. (Enter your answers as a comma-separated list. Enter your answers from smallest to largest.) 077 707 77 7 λ; = For each eigenvalue, find the dimension of the corresponding eigenspace. (Enter your answers as a comma-separated list.) dim(x;) =arrow_forward
- Find the eigenvalues of the symmetric matrix. (Enter your answers as a comma-separated list. Enter your answers from smallest to largest.) λ; = 07 77 For each eigenvalue, find the dimension of the corresponding eigenspace. (Enter your answers as a comma-separated list.) dim(x) = 6 Need Help? Read It Xarrow_forwardFor the matrix A, find (if possible) a nonsingular matrix P such that P-1AP is diagonal. (If not possible, enter IMPOSSIBLE.) 1 2 4 1 2 P = A = I P-¹AP = N|H m/~ 3 -1 Verify that P-1AP is a diagonal matrix with the eigenvalues on the main diagonal.arrow_forwardConstruct a symmetric matrix A with eigenvalues A1 = -3 and 2 = 7 and 1 and V2 = corresponding orthogonal eigenvectors V1 %3D 1 a11 a12 respectively. If A , then the value of a11 is a21 a22 , the value of A12 is A, the value of a21 is and the value of A22 isarrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY 
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,