
A First Course in Probability (10th Edition)
10th Edition
ISBN: 9780134753119
Author: Sheldon Ross
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Question
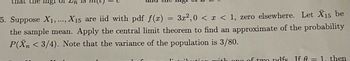
Transcribed Image Text:mgi u
5. Suppose X₁,..., X15 are iid with pdf f(x) = 3x²,0 < x < 1, zero elsewhere. Let X15 be
the sample mean. Apply the central limit theorem to find an approximate of the probability
P(Xn <3/4). Note that the variance of the population is 3/80.
on with one of two pdfs If A = 1. then
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps

Knowledge Booster
Similar questions
- Let x = age in years of a rural Quebec woman at the time of her first marriage. In the year 1941, the population variance of x was approximately ?2 = 5.1. Suppose a recent study of age at first marriage for a random sample of 41 women in rural Quebec gave a sample variance s2 = 2.9. Use a 5% level of significance to test the claim that the current variance is less than 5.1. Find the value of the chi-square statistic for the sample. (Round your answer to two decimal places.) What are the degrees of freedom?arrow_forwardSuppose a population has a standard deviation of 10. Assume that we continue to select groups of 100 individuals from the population and calculate the sample means. The variation among all these sample means is measured by o/v(n). Compare the distribution of single observations (x) with that of the means x. (That is, compare the histograms of x and x.) We can conclude that the distribution of x is spread out. In other words, averages vary much than individual observations. less; less less; more more; less more; morearrow_forwardConsider the variable X whose mean and variance are given respectively by μx = 28.4 and Var(X) =8.6. Next consider the variable Y such that Y = 18.6 X-52 What is the mean of variable Y?arrow_forward
- The average height X and weight Y of males in population have a bivariate normal distribution with means µX 1.80 m., µy 90.0 kgs and standard deviations Ox = 0.30 m., oy = 15.3 kgs respectively. The correlation coefficient between X and Y is p= 0.80.arrow_forwardLet L be the random variable for the length of time, in years, that a person will remember an actuarial statistic. For a certain popula- tion, L is exponentially distributed with mean 1/Y, where Y has a gamma distribution with a = 4.5 and 3 = 4. Find the variance of L.arrow_forwardLet S1^2 be the sampling variance for a random sample of twelve values (amount of mercury in the blood) and let S2^2 be the sampling variance for a random sample of ten values (amount of lead in the blood); samples from the same population were used. The population variance for mercury measurements is assumed to be twice the corresponding population variance for lead measurements. We will further assume that S1^2 is independent of S2^2. 1. Find a number b such that P [(S1^2/S2^2)<=b]=0.95 enter such a b to three decimal places b= 2. Consider the number b calculated above, find a number a such that P[a<=(S1^2/S2^2)<=b]=0.90 enter said a to three decimal places. a=arrow_forward
- Suppose that Y has an exponential distribution with mean Beta. Show that 2Y/Beta has a chi square distribution with 2 degrees of freedom.arrow_forwardSuppose that the duration of a particular type of criminal trial is known to be normally distributed with a mean of 20 days and a standard deviation of 5 days. Let X be the number of days for a randomly selected trial. Round all answers to 4 decimal places where possible.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 A First Course in Probability (10th Edition)ProbabilityISBN:9780134753119Author:Sheldon RossPublisher:PEARSON
A First Course in Probability (10th Edition)ProbabilityISBN:9780134753119Author:Sheldon RossPublisher:PEARSON

A First Course in Probability (10th Edition)
Probability
ISBN:9780134753119
Author:Sheldon Ross
Publisher:PEARSON
