
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Concept explainers
Topic Video
Question
thumb_up100%

Transcribed Image Text:Suppose we prove that
2" > n?
for n=1 and 2. Knowing that the inequality is true for some n
n > 4
and we can show that it must be true for n+1 instead of n, can we conclude that
2" > n2
is true for all
n > 1
?
True
False
Expert Solution
arrow_forward
Step 1
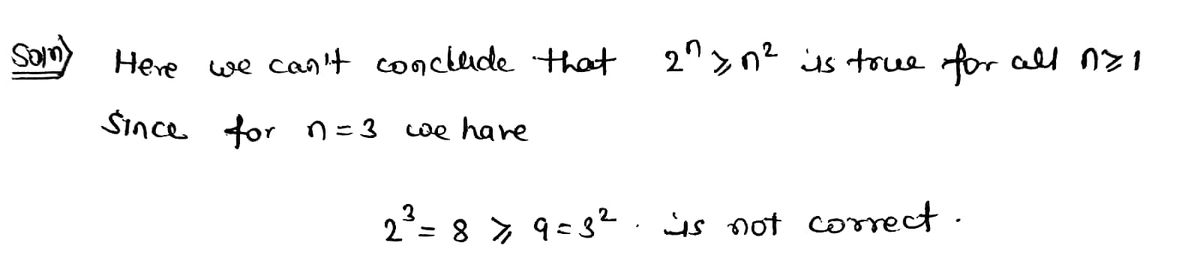
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- 3. (Р5, Раge 16; Prove that a <0. (You may have to use Proof by Contradiction and Archimedean Property, Part ii.) Suppose that the number a has the property that for every natural number n, a < 1/n.arrow_forwardShow your workarrow_forwardOption 3 Q8. For which positive integer values of n is true? 1 1 n+2 O O O O ≤ 0.02014 < O Option 1 n=48,49 O Option 2 n=58,49 O Option 3 n-68,49 n=78,49 O Option 4 Q9. Solve -|S Option 4 narrow_forward
- 2. Solve for neN using a product of factors not the ! function on the calculator. Show steps. 9! a) n = 7!3! (n+4)! %3D b) 5 = (n+3)!arrow_forwardI need some help with this problem which involves the difference between three integersarrow_forward5. In Algebra you are taught that for any real numbers a > 0 and x that the inequality -a 0), if -aarrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

