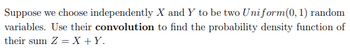
Suppose we choose independently X and Y to be two Uniform(0, 1) random variables. Use their convolution to find the probability density function of their sum Z = X + Y.

The probability density of the random variable Z isgiven by f(z) = kze−z2for z > 00 for z F 0Find k and draw the graph of this probability density.

Let X1 and X2 be two continuous random variableshaving the joint probability density f(x1, x2) = 4x1x2 for 0 < x1 < 1, 0 < x2 < 10 elsewhereFind the joint probability density of Y1 = X21 and Y2 = X1X2.

The life expectancy of a smartphone's battery X in days is a continuous random variable with probability density function fx=6x1-x for 0 ≤ q x ≤ q 1. Find the probability that a smartphone chosen at random will have a life expectancy exceeding 12 hours.

If X has an exponential distribution with the param-eter θ, use the distribution function technique to find the probability density of the random variableY = ln X.

Let X be a random variable with uniform distribution on the interval [-2,2]. Let Y be defined as Y = X5. Calculate the pdf of Y.

10) Let f(x) by the probability density function of some continuous random variable. Explain why it must be true that f(x) dx =1.

Suppose that X and Y have a joint probability density function given by ce-3z-5y if r, y 20 fx.x(T, y) = otherwise Are the random variables X and Y statistically independent? Justify your answer.

Let y be the random variable with the time to hear an owl from your room's open window (in hours). Assume that the probability that you still need to wait to hear the owl after y hours is one of the following: the probability is given by 0. 47e-4y + 0. 52e-5y Find the probability that you need to wait between 2 and 4 hours to hear the owl, compute and display the probability density function graph as well as a histogram by the minute. Compute and display in the graphics the mean, variance, and quartiles of the waiting times. Please pay attention to the various units of time!

let X denotes the percentage of time out of a 40-hour workweek that a call center agent is directly serving a client by answering phone calls. Suppose that X has a probability density function defined by f(x) =3x² for 0 ≤ x ≤ 1. Find the mean and variance of X. Interpret the results.