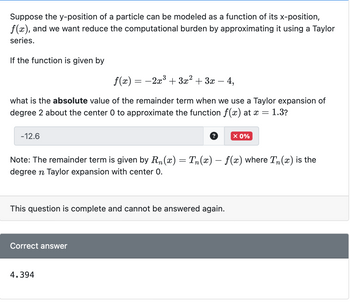
Suppose the y-position of a particle can be modeled as a function of its x-position, f(x), and we want reduce the computational burden by approximating it using a Taylor series. If the function is given by f(x) = −2x³ + 3x² + 3x 4, what is the absolute value of the remainder term when we use a Taylor expansion of degree 2 about the center 0 to approximate the function f(x) at x = 1.3? -12.6 Note: The remainder term is given by Rn(x) = Tn(x) − ƒ(x) where Tɲ(x) is the degree n Taylor expansion with center 0. This question is complete and cannot be answered again. Correct answer X 0% 4.394

Simplify the following...  27 2/3 32 4/5

Using the Definition of am/n Simplify:a. 272/3 b. 93/2 c. 81-3/4.

process. 530.16682543 Jump to level 1 Let U2 be a basis for a subspace of IR2X2 12 the Gram-Schmidt process to find an orthogonal pasis under the Frobenjus inner product. 1.38 Orthogonal basis Ex: 5 b= Ex 5 4. Check