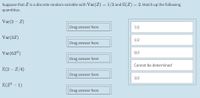
Suppose that Z is a discrete random variable with Var(Z) = 1/2 a quantities. %3D Var(2 – Z) Drag answer here Var(3Z) Drag answer here Var(67²) Drag answer here

2. Need help

Suppose X and Y are independent. X has a mean of 1 and variance of 1, Y has a mean of 0, and variance of 2. Let S=X+Y, calculate E(S) and Var(S). Let Z=2Y^2+1/2 X+1 calculate E(Z). Hint: for any random variable X, we have Var(X)=E(X-E(X))^2=E(X^2 )-(E(X))^2, you may want to find EY^2  with this. Calculate cov(S,X). Hint: similarly, we have cov(Z,X)=E(ZX)-E(Z)E(X), Calculate cov(Z,X). Are Z and X independent? Are Z and Y independent? Why? What about mean independence?

Really need it to study, please don't copy the answers from other

Determine the mean and the variance for the (continuous) random variables with the following moment-generating function: M(t) = (1 – 4t)-2

X and Y are random variables that are the same normally distributed variables as in the previous problem. The Mean of X is 5 and its SD is 3. The Mean of Y is -2 and its SD is 6. You are now being told they are independent. Find the value of each requested parameter. The mean of T= - 3x + 20 is The mean of W= Y - X is The variance of D= X - 2Y is

2. Confidence interval σ knownDr. Patton is a professor of English. Recently she counted the number of misspelled words in a group of student essays. She noted the distribution of misspelled words per essay followed a normal distribution with the population standard deviation of 2.4a words per essay. For her Tuesday class of 40 students, the mean number of misspelled words per essay was 6.05. Construct a 95% confidence interval for the mean number of misspelled words in the population of students’ essays. (a=1)

Suppose that X is a random variable for which the m.g.f. is as follows: M(t) = 1/4(3et+e-t), -∞<t<∞  Find the mean and variance of X.

Let X1 and X2 be two independent random variables with common mean E(X1) = E(X2) = µ. The variance of X1 is 1 and the variance of X2 is 16. Consider estimators of u described by û = W1X1 + W2X2 for some constants w1 and w2 that you can choose. (a) Say that w2 the estimate unbiased for all w1? = a – bw1 for some constants a and b. What values of a and b would make

Find variance of Y1