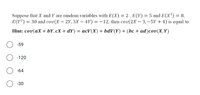
Suppose that X and Y are random variables with E(X) = 2 , E(Y) = 5 and E(X²) = 8, E(Y²) = 30 and cov(X – 2Y,3X – 4Y) =-12, then cov(2X – 3, –5Y + 4) is equal to: Hint: cov(aX + bY,cX + dY) = acV(X) + bdV(Y) + (bc + ad)cov(X,Y) -59 -120 -64 -30

C2. Let X and Y be random variables, and let a and b be constants. (a) Starting from the definition of covariance, show that Cov(aX, Y): = a Cov(X, Y). You may find it helpful to remember that if EX = µx, then EaX = αμχ· (b) Show that Cov(X + b, Y) = Cov(X, Y). Now let X, Y, Z be independent random variables with common variance o². (c) Find the value of Corr(2X - 3Y + 4, 2Y – Z - 1). You may use any facts about covariance from the notes, including those from parts (a) and (b) of this question, provided you state them clearly.

For two random variables X and Y, we have Var(X) = 8, Var(Y) = 4, Cov(X, Y) = -2. Find the values of the following quantities. Please show your work. (a) Cov(Y, X) (Hint: by using the definition Cov(X, Y) = E[(X – EX)(Y – EY)], observe that Cov(X, Y) = Cov(Y, X). ] (b) Cov(X, X) (Hint: by using the definition of covariance and variance, observe that Cov(X, X) = Var(X). ) (c) Var(X + Y) (Hint: use the identity Var(X + Y) = (d) Var(X + X) Var(X)+ Var(Y) + 2Cov(X, Y). ) (e) Cov(X, -X) (Hint: use the identity Cov(aX, bY) = ab · Cov(X,Y). )

2. Let X and Y be random variables, and let a and b be constants. (a) Starting from the definition of covariance, show that Cov(aX,Y) = a Cov(X,Y). You may find it helpful to remember that if EX = µx, then EaX = aux. (b) Show that Cov(X + b, Y) = Cov(X,Y). Now let X, Y, Z be independent random variables with common variance o?. (c) Find the value of Corr(2X – 3Y + 4, 2Y – Z – 1). You may use any facts about covariance from - the notes, including those from parts (a) and (b) of this question, provided you state them clearly.