Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN: 9781133382119
Author: Swokowski
Publisher: Cengage
expand_more
expand_more
format_list_bulleted
Related questions
Question
thumb_up100%
Solve given problem:
Transcribed Image Text:7. Suppose that the sequence \((a_n)\) converges to \(a\) and that \(|a| < 1\). Prove that the sequence \((a_n)^n\) converges to 0.
Expert Solution
arrow_forward
Step 1
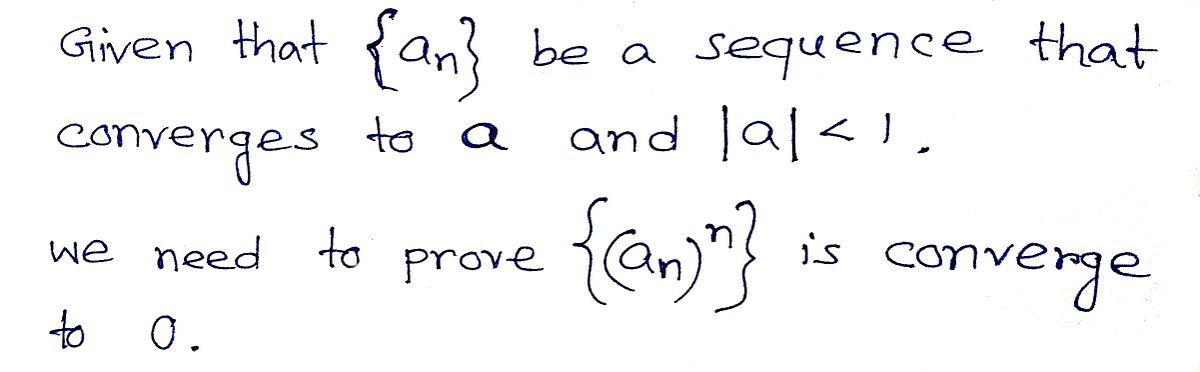
Step by stepSolved in 3 steps with 3 images
Knowledge Booster
Similar questions
- Find the limit of the sequencearrow_forwardSuppose that an-> L and bn-> L. Show that the sequence a1, b2, a2, b2, a3, b3.... converges to L.arrow_forward1. Let a, = 1 and an+1 = 1+ 1+an (a) Find the first six terms of the sequence {an}. (b) Prove that {an} is bounded. (c) Prove that {a1,a3,a5, ... , A2n+1» …..} is increasing and {a2, a4, a6, ... , a2n, ...} is decreasing. (d) Find lim an.arrow_forward
- Prove that the sequence {cn} converges to c if and only if the sequence {cn- c} converges to 0.arrow_forwardLet (a_n)be the sequence defined by the recursive relation a_n=na_(n−1), with initial term a0=1.Use iteration to find a closed formula for the sequence. Simplify your answer whenever possible.arrow_forwardUse the definition to prove that {(-1)"} is not a Cauchy sequence.arrow_forward
- Let (a_n) be the sequence defined by the recursive relation a_n=a_(n−1)+5n+1, with initial term a0=0.Use iteration to find a closed formula for the sequence. Simplify your answer whenever possible.arrow_forwardSuppose ao, a1, a2,... is a sequence such that ao = a1 = 1 and forn2 1, an+1 = n(an+an-1). Find az = a5 = -, a7 =arrow_forwardLet {an} be a monotonic sequence such that an ≤ 1. Discuss the convergence of {an}. When {an} converges, what can you conclude about its limit?arrow_forward
- a) {(SN +17)/(2N)} 10. Prove that the sequence {(-1)"} does not converge. 11. (r.} be aarrow_forwardPLEASE DO NOT prove by contradiction. Thank you very much!arrow_forward2) Show that the sequence defined recursively by 3 4 An aj = 5 аn+1 satisfies 2 < an < 5 and is decreasing. Show that the sequence is convergent and find its limit.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage