Suppose temperature °F in a region of 3-space, measured in meters, is given by T= 100 1+ (x − 3)² + y² + (z + 2)² and a bug is a point (2, 1,-1). (a) What direction should the bug fly when attracted to heat? (b) Find the components of a vector that starts at (2,1,-1) and ends at (3, 0, -2). Is this in the same direction as the převious answer? Physically, why fly towards (3, 0, -2)? (c) What is the rate of change of temperature at (2, 1, -1) when flying towards the heat? (decimal answer and include units) (d) What direction is the most rapid decrease in temperature?

Suppose temperature °F in a region of 3-space, measured in meters, is given by T= 100 1+ (x − 3)² + y² + (z + 2)² and a bug is a point (2, 1,-1). (a) What direction should the bug fly when attracted to heat? (b) Find the components of a vector that starts at (2,1,-1) and ends at (3, 0, -2). Is this in the same direction as the převious answer? Physically, why fly towards (3, 0, -2)? (c) What is the rate of change of temperature at (2, 1, -1) when flying towards the heat? (decimal answer and include units) (d) What direction is the most rapid decrease in temperature?

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Related questions

Q: 13. Find a vector equation of the line through (2, 1) parallel to (x, y) = (-2,7)+t(3,5). 14. Find a…

Q: How would I find the equation of the line through points (1,2,0) and (1,4,1) in parametric vector…

Q: 8. A line e is parallel to the vector 2i- 2j + k and passes through the point A with position vector…

A: The plane's normal vector is 3i-4j-k and a position vector passes through it is -i+4k. The vector…

Q: Find parametric equations for the line whose vector equation is given. (a) (x, y) = (4, –6) + t(1,…

Q: Find a scalar equation of the plane containing the line and the point (-5, -1,5). x = 6 +8t, y=-1-3t…

Q: Find the angle between the planes whose vector equations are 7-(2i + 2)- 36) =57-(3i -3) + Sk) = 3…

A: The solution to the the given question is explained below.

Q: A vector equation for the line through the points A (3, -4, -3) and B (3,4,2) is (x, y, z) = . (You…

A: Concept to be used:If a line passes through two points A,Bwith position vectors aand brespectively,…

Q: T₁: 2x-y+2z=6 And T₂:X-y+4

Q: I reached this same conclusion " Tx=Ax1x2⇒Tx=0110x1x2⇒Tx=x2x1" but had difficulty explaining it in…

A: It can be proven that if x=x1x2∈ℝ2, then Tx=Ax=x2x1 where T is the linear transformation whose…

Q: A particle moves in two dimensional space where i and į are unit vectors in the x and y directions…

A: given r→=6t-4t2i^+2t j^ a) write down the particle's velocity vector in component form. ii) find…

Q: Find the velocity vector v(t), given the acceleration vector a(t) = (3e¹, (Use symbolic notation and…

A: Formula for the acceleration is We have and the initial velocity

Q: Which vector equation below represents the line in R³ that passes through the point (-4, 5, 7) and…

Q: Given the graph of the polynomial function, determine its equation: 6- 4 2- 0 -2- -4- H 2 3 4 X

Q: For this problem, enter your vectors with angle-bracket notation: , not in ijk- notation. (a) F =…

A: The solution are next step

Q: (14) The straight line L passes through the origin O and is in the direction i+mj. The straight line…

Q: Find the scalar equation for each line: (a) a line through the point (-6, 7) with direction vector…

A: Since you have asked multiple question, we will solve the first question for you as per our guide…

Q: At time t=0, a particle is located at the point (3,9,4). It travels in a straight line to the point…

Q: Find the rotation matrix of a linear transformation T: R² R2, which first rotates points 3 clockwise…

Q: The velocity vector of a particle in the xy-plane is (√7, 9e³-3) for all real t. If the position of…

A: The velocity vector in the xy-plane is for all real t. If the position of theparticle at , then to…

Q: Consider A = (0, 4, 2), B = (6, -1, 0) and C = (3, 0, 1). (i) Find the unit vector having the same…

A: We have to find the unit vector having the same direction as B-2A+12C Then, we can proceed further.

Q: Draw the vectors in standard position in R2 with their tails at the point (2, -3).

Question

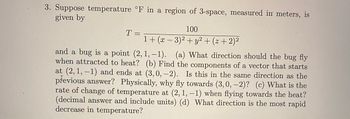
3. Suppose temperature °F in a region of 3-space, measured in meters, is
given by
T =
100
1+ (x − 3)² + y² + (z + 2)²
and a bug is a point (2, 1,-1). (a) What direction should the bug fly
when attracted to heat? (b) Find the components of a vector that starts
at (2, 1, -1) and ends at (3, 0, -2). Is this in the same direction as the
previous answer? Physically, why fly towards (3,0,-2)? (c) What is the
rate of change of temperature at (2, 1, -1) when flying towards the heat?
(decimal answer and include units) (d) What direction is the most rapid
decrease in temperature?

Expert Solution

Step 1

Given:

$T = \frac{100}{1 + {(x + 3)}^{2} + y^{2} + {(z + 2)}^{2}}$

Where T is the temperature function.

Position of the bug = (2, 1, -1)

To find:

We have to find the direction of the bug when flying towards the heat.

We can find the direction of attraction to heat by finding the gradient of the temperature function by the following formula:

$\begin{array}{rcl} \nabla T & = & \frac{\partial T}{\partial x}, \frac{\partial T}{\partial y}, \frac{\partial T}{\partial z} \end{array}$

Step by step

Solved in 5 steps

SEE SOLUTION Check out a sample Q&A here

Similar questions

Suppose the straight lines L₁ and L₂ have respective vector equations 5 r1 = -3 + t -0-0--0- and 4 3 where s and t are scalar parameters. 9 = 8 +s -2 -5 -5 2 a) Given that L₁ and L2 intersect at some point P, find its coordinates. P =( )
Write down the vector equation of the line that passes through the points (x,y,z) = (2,3,7) and (x,y,z)= (4,1,2)
A PARTICLE MOVES WITH A SPEED OF 2 m/s IN THE DIRECTION OF THE VECTOR a=(5,-3,2) determine the x, y, and z components of the velocity vector
the space curve (t) = (2t, t², 2t)
Solve the following equations show your solutions. 1. Given the line 2x = 5y + 9. Find its equation in intercept/s form. 2. Determine the divergence of the vector: V = i(x^2)y + j(-xy) + k(xyz) at coordinates (3, 2, 1). 3. If "n" is any positive integer, then (n - 1)(n - 2)(n - 3)...(3)(2)(1) = ?
16. Find both the vector equation and the parametric equations of the line through (-2,2,8) and (1, - 4,0), where t =0 corresponds to the first given point. The vector equation is (x,y,z) = + (1). Find the parametric equations of the line through (-2,2,8) in the direction from (-2,2,8) toward (1,-4,0). The parametric equations are x = (Use the answer from the previous step to find this answer.) y%3D (1) O t(3,-6,-8). O t(-6,3,-8). O t(-8,-6,3). O t(-8,3,-6). 17. If possible, find the absolute maximum and minimum values of the following function on the region R. f(x,y) = 5 e-X-Y; R={(x,y): x20, y2 0} Determine the absolute maximum value of f(x,y) on R. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. The absolute maximum value of f on R is O B. The function f(x,y) has no absolute maximum value on R. Determine the absolute minimum value of f(x,y) on R. Select the correct choice below and, if necessary, fill in the answer box to…
Determine the vector equation for the line that is parallel to 7 = [1,5,-7]+t[2,-1,5] with the same x-intercept as [x, y, z]=[-1,8,6]+t[-2,4,3]. 3.