
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
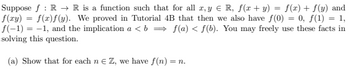
Transcribed Image Text:Suppose f: R → R is a function such that for all x, y ≤ R, f(x + y) = f(x) + f(y) and
f(xy) = f(x)f(y). We proved in Tutorial 4B that then we also have f(0) = 0, f(1) = 1,
f(-1) = -1, and the implication a<b⇒ f(a) < f(b). You may freely use these facts in
solving this question.
(a) Show that for each n = Z, we have f(n) = n.
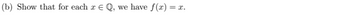
Transcribed Image Text:(b) Show that for each z E Q, we have f(x) = x.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 2 images

Knowledge Booster
Similar questions
- 3. (a) (b) Let f: X→ Y and g: Y→ Z be functions. Prove the following statements. If f and g are both injective, then go f is injective. If f and g are both surjective, then go f is surjective. (c) If ƒ and g are both bijective, then go f is bijective.arrow_forward(2) Let f(x) = ax³ + bx? + cr + d, where a, b, c, d e R and a + 0. Prove that f(x) must have a root. That is, prove f(z) = 0 for some z € R.arrow_forwardSuppose fn → f and the functions fn all satisfy the Lipschitz condition |fn(x) – fn(y)| < M|x – y| for some constant M in- dependent of n. Prove that f also satisfies the same Lipschitz condition.arrow_forward
- Suppose fR → R is a function such that for all x, y € R, f(x + y) = f(x) + f(y) and f(xy) = f(x)f(y). We proved in Tutorial 4B that then we also have f(0) = 0, f(1) = 1, f(-1) = -1, and the implication a < b ⇒ f(a) < f(b). You may freely use these facts in solving this question. (a) Show that for each n = Z, we have f(n) = n. (b) Show that for each z EQ, we have f(x) = x. (c) Let A CR, and write f(A) for the set {r Ry & A: f(y) = x}. Show: if A is bounded above, then f(A) is bounded above. (d) Let A CR be bounded above, with supremum L. Show that f(L) is the supremum of f(A). (e) Now use the statements proved in the previous parts to prove: for all a R, we have f(x) = x.arrow_forward5. Find f og and g•f , where f(x) = x² + 1 and g(x) = x + 2, are functions from R to R.arrow_forwardShow that the function f : R – {3} → R – {5} defined by f(x) = *, is bijective and determine f-(x) for x eR – {5}.arrow_forward
- we have f: X→Y is a 1-1 function and Y is countable. Since f is 1-1, is it correct that this implies X ~ f(X) [which is f:X →f(X)] which further implies bijecton? Also, does this imply f(X) ⊆ Y?arrow_forwardSuppose f: R → R is a function such that for all x, y ≤ R, f(x + y) = f(x) + f(y) and f(xy) = f(x)f(y). We proved in Tutorial 4B that then we also have f(0) = 0, f(1) = 1, f(-1) = -1, and the implication aarrow_forwardConsider a function f: (0, 1) → (0, 1] defined as follows: Sx, if x {2":ne N}, N and x = = 2-2. if n f(x) = Then f is a bijection. True False 2¹-narrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

