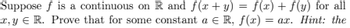
Suppose f is a continuous on R and f(x + y) = f(x) + f(y) for all r,y R. Prove that for some constant a € R, f(x) = ax. Hint: the

What is Continuous Function:

In mathematics, a continuous function is one that, in response to a continuous variation—a change in the argument without a jump—causes the value of the function to vary continuously. This shows that there are no abrupt changes in value or discontinuities. More exactly, a function is continuous if it is possible to guarantee that, even with arbitrarily small changes to its parameter, its value won't change dramatically. Any function that is discontinuous is referred to as such.

Given:

Given that $f$ is continuous on $\mathrm{ℝ}$ satisfying $f\left(x+y\right)=f\left(x\right)+f\left(y\right)$ for all $x,y\in \mathrm{ℝ}$.

To Prove:

We show that for some constant $a\in \mathrm{ℝ}$, $f\left(x\right)=ax$.