
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
Suppose {an} ∞ n=1 and {bn} ∞ n=1 are sequences such that {an} ∞ n=1 and {an + bn} ∞ n=1 converge. Prove that {bn} ∞ n=1 converges.
Expert Solution
arrow_forward
Step 1
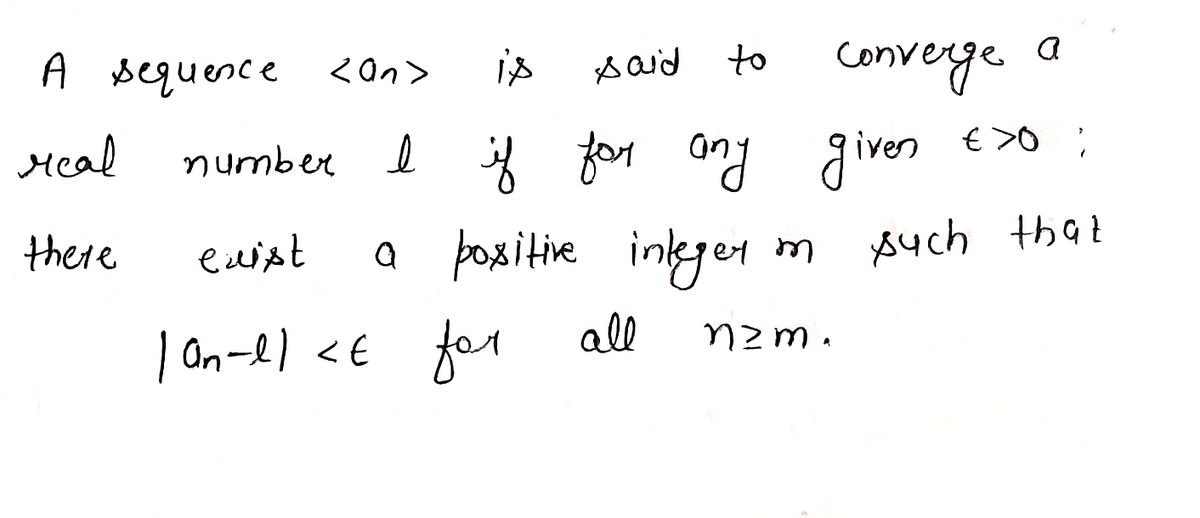
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- 2 Show that the sequence defined by, 1 ад 3D 1, ап+1 %3 3 an | is convergent. (Hint: Use the induction method to prove monotonicity.)arrow_forwardSuppose {fn}n=1 converges uniformly on E. Show {fn=1 converges pointwise on E.arrow_forwardShow that the sequence (1/nk) nen is convergent if and only if k ≥ 0, nEN and that the limit is 0 for all k > 0.arrow_forward
- Write out the first five terms of the sequence with, In(n) determine whether the sequence n+1 n=1 converges, and if so find its limit. In(n) Enter the following information for an = n+1 · аз a4 a5 In(n) lim n→00 n +1 |||| ||arrow_forwardLet a1 = 1 and an+1 = [1-1/(n+1)^2]an for all n ≥ 1. 1) Show that the sequence {an}n≥1 converges. 2) Find its limitarrow_forwardto determine if it converges of divergesarrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

