
MATLAB: An Introduction with Applications
6th Edition
ISBN: 9781119256830
Author: Amos Gilat
Publisher: John Wiley & Sons Inc
expand_more
expand_more
format_list_bulleted
Question
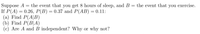
Transcribed Image Text:Suppose A
=
the event that you get 8 hours of sleep, and B = the event that you exercise.
: 0.26, P(B) = 0.37 and P(AB) = 0.11:
If P(A):
=
(a) Find P(A|B)
(b) Find P(BA)
(c) Are A and B independent? Why or why not?
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 3 steps with 2 images

Knowledge Booster
Similar questions
- When a man observed a sobriety checkpoint conducted by a police department, he saw 656 drivers were screened and 5 were arrested for driving while intoxicated. Based on those results, we can estimate that P(W) = 0.00762, where W denotes the event of screening a driver and getting someone who intoxicated. What does P (W) denote, and what is its value? What does P(W) represent? CA. P(W) denotes the probability of screening a driver and finding that he or she is not intoxicated. O B. P(W) denotes the probability of a driver passing through the sobriety checkpoint. O C. P(W) denotes the probability of screening a driver and finding that he or she is intoxicated. O D. P(W) denotes the probability of driver being intoxicated. P(W) =| (Round to five decimal places as needed.)arrow_forwardThe Statistical Abstract of the United States reported that 66% of students who graduated from high school in 2012 enrolled in college. Let X be the number of high school students that enrolled in college. Formulas needed: E (X) = n * p and Var (X) = n * p * (1 − p) - a) If exactly 18 high school students are chosen at random, the expected number of high school students are enrolle in college is Round your answer to next whole number. b) If exactly 18 high school students are chosen at random, the std(X), standard deviation of the number of them that are enrolled in college is Round your answer to the nearest whole number.arrow_forwardWhen a man observed a sobriety checkpoint conducted by a police department, he saw 667 drivers were screened and 4 were arrested for driving while intoxicated. Based on those results, we can estimate that P(W) = 0.00600, where W denotes the event of screening a driver and getting someone who is intoxicated. What does P (W) denote, and what is its value? What does P(W) represent? O A. P(W) denotes the probability of a driver passing through the sobriety checkpoint. O B. P(W) denotes the probability of driver being intoxicated. O C. P(W) denotes the probability of screening a driver and finding that he or she is not intoxicated. O D. P(W) denotes the probability of screening a driver and finding that he or she is intoxicated. P(W) =O (Round to five decimal places as needed.)arrow_forward
- A commuter must pass through three traffic lights on her way to work. For each traffic light, the probability that it is green when she arrives is 0.6. The lights are independent. 3 (a) Compute the probability that all three lights are green. (b) The commuter goes to work five days per week. Let X be the number of times out of the five days in a given week that all three lights are green. Assume the days are independent of one another. Determine the distribution of X. (c) Calculate P(X= 3).arrow_forwardSuppose the probability that a male develops some form of cancer in his lifetime is 0.4573. Suppose the probability that a male has at least one false positive test result (meaning the test comes back for cancer when the man does not have it) is 0.51, and that this probability is independent of the probability that a male will develop cancer in his lifetime. • C = a man develops cancer in his lifetime• F = a man has at least one false positive Part (a) Construct a tree diagram of the situation. P(C) = P(F | C) = P(F | C' ) If a test comes up positive, based upon numerical values, can you assume that man has cancer? Justify numerically and explain why or why not. -You cannot assume the man has cancer because there is not enough information given. -You cannot assume the man has cancer because there is a 51% chance that the test is false. -You cannot assume the man has cancer because both the probability of developing cancer in his lifetime and the probability of…arrow_forwardWhen a man observed a sobriety checkpoint conducted by a police department, he saw 656 drivers were screened and 5 were arrested for driving while intoxicated. Based on those results, we can estimate that P(W)equals=0.00762,where W denotes the event of screening a driver and getting someone who is intoxicated. What does P(W) denote, and what is its value? What does P(W) represent? P(W)=arrow_forward
- Suppose that in a year of 365 days, it rains on 62 days. There is lightning on 13 days. There is both lightning and rain on 12 days. Compare the chance that a rainy day has lightning to the chance that a day with lightning has rain. Show your work here P(lightning | rain) = P(rain | lightning)arrow_forwardFor this problem, assume that 11 % withdraw, 14 % receive an A, 18 % receive a B, 35 % receive a C, 14 % receive a D, and 8 % receive an F. (1) What probability should be assigned to the event "pass the course"? (2) What probability should be assigned to the event "withdraw or fail the course"?arrow_forwardSuppose you are deciding whether or not to bring an umbrella to school and the weathercan be either sunny or rainy. Initially, you think the probability that it will be sunny isP (S) = 0.6, and the probability that it will be rainy is P (R) = 0.4. If you bring an umbrellaand it rains, your payoff is 6. If you bring an umbrella and it is sunny, your payoff is 9. Ifyou don’t bring an umbrella and it rains, your payoff is 0. If you don’t bring an umbrellaand it is sunny, your payoff is 10. Suppose that you check two websites for weather forecasts.You know that the two forecasts are independent of each other, and each forecast is correct70% of the time. That is, the probability that the website says it will be sunny given that itactually will be sunny is 0.7, and the probability that the website says it will rain given thatit actually will rain is 0.7. Suppose that you suffer from confirmation bias. You initially thinkit is more likely to be sunny, so you misinterpret rain forecasts as sun…arrow_forward
- Sarah and Thomas are going bowling. The probability that Sarah scores more than 175 is 0.5 , and the probability that Thomas scores more than 175 is 0.1 . Their scores are independent. Round your answers to four decimal places, if necessary. (a) Find the probability that both score more than 175 . (b) Given that Thomas scores more than 175 , the probability that Sarah scores higher than Thomas is 0.4 . Find the probability that Thomas scores more than 175 and Sarah scores higher than Thomas.arrow_forwardwhich expressions correctly describes the experimental probability, P(B), where n(B) is the number of times event B occurred and n(T) is the total number of trials, T, in the experiment? a) P(B) = n(B) x n(T) b) P(B) = n(N) + n(T) c) P(B) = n(T)/n(B) d) P(B) = n(B)/n(T)arrow_forwardThe route used by a certain motorist in commuting to work contains two intersections with traffic signals. The probability that he must stop at the first signal is 0.45, the analogous probability for the second signal is 0.5, and the probability that he must stop at at least one of the two signals is 0.9. (a) What is the probability that he must stop at both signals? X (b) What is the probability that he must stop at the first signal but not at the second one? X (c) What is the probability that he must stop at exactly one signal?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman

MATLAB: An Introduction with Applications
Statistics
ISBN:9781119256830
Author:Amos Gilat
Publisher:John Wiley & Sons Inc

Probability and Statistics for Engineering and th...
Statistics
ISBN:9781305251809
Author:Jay L. Devore
Publisher:Cengage Learning

Statistics for The Behavioral Sciences (MindTap C...
Statistics
ISBN:9781305504912
Author:Frederick J Gravetter, Larry B. Wallnau
Publisher:Cengage Learning

Elementary Statistics: Picturing the World (7th E...
Statistics
ISBN:9780134683416
Author:Ron Larson, Betsy Farber
Publisher:PEARSON

The Basic Practice of Statistics
Statistics
ISBN:9781319042578
Author:David S. Moore, William I. Notz, Michael A. Fligner
Publisher:W. H. Freeman

Introduction to the Practice of Statistics
Statistics
ISBN:9781319013387
Author:David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:W. H. Freeman