
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
Transcribed Image Text:MAA
MATHEMATICAL ASSOCIATION OF AMERICA
Previous Problem Problem List Next Problem
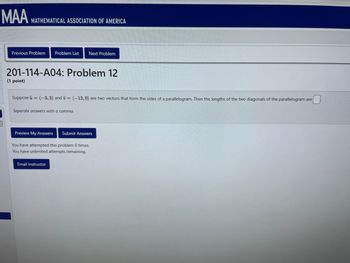
201-114-A04: Problem 12
(1 point)
Suppose = (-3, 3) and = (-12, 0) are two vectors that form the sides of a parallelogram. Then the lengths of the two diagonals of the parallelogram are
Separate answers with a comma.
Preview My Answers Submit Answers
You have attempted this problem 0 times.
You have unlimited attempts remaining.
Email Instructor
Expert Solution
arrow_forward
Step 1
The sum of the vectors
The points to the vertex of the parallelogram are opposite to the origin.
Its distance from the origin is the length of one of the diagonals:
So,
So, length of one diagonal is
Step by stepSolved in 2 steps

Knowledge Booster
Similar questions
- if given the equation yi = B0 + B1xi +ui and express the same equation as y = xiB = ui (where xi and B here are vectors), does vector xi = [1 x1] or xi = [x1] (row vector) and B vector (column vector) = [B0; B1]?arrow_forwardplease answerarrow_forwardShow whether or not the diagonals of parallelogram ABCD bisect each other given A(-2,2), B(1,4), C(2,8) and D(-1,6).arrow_forward
- Find the sum and difference of the following vectors: a. <-4,6>+<5,0> b. <-7,5>0<-5,-9>arrow_forwardAssume v1 = [3,-2] and v2 = [-1,4]. Find the sum and difference of vectors v1 and v2. v1 + v2 = [Answer,Answer] v1 − v2 = [Answer,Answer]arrow_forwardGiven vectors a = (3, -5) and b = (-2, 7), find 4a - 5barrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

