Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
Subtiers or Series Limit Type Tier Expression Notes Examples Convergence Two examples Super Large an = n" N/A among many an = n! тп 3" Larger |q|, Exponentially Large An = q", |q| > 1 en larger tier (-2)" (3/2)" nº lim an = ∞ ±an n2 Positive n=1 Larger s, larger tier an = n°, п Power Diverges Vn n'/3 [In(n)]² In(n) Positive Logarithmic Power an = [In(n)]*, s > 0 Larger s, larger tier [In(n)]}/2 Both an and 1/an are bounded 2n Bounded e.g. an — C #0, ап — (-1)", аn %3D n+1 Negative Logarithmic Power In(n)]-1/2 1/ In(n) [In(n)]-2 1/Vn An = [In(n)]ª, Larger s, larger tier ±an n=1 Diverges Or Converges Conditionally" n-1 Negative Power Larger s, larger tier an =n°, Twilight Realm -1.0000001 n-2 lim an = 0 (1/2)" e-n Exponentially Small An = q", 0 < [q| < 1 Larger |q|, larger tier an 1/(-3)" n=1 Converges Absolutely Two examples an = e" /n! Super Small N/A among many An =n-n Zero An = 0 Smallest (2) With the help of the "tierlist", sort the following sequences in descending order: In dn fn en ba Сп e" - (-4)" | т'" | sin(-n) + (-1)" ап n° е—п n2 +n-" (-1)" + 3/In(n) п—е

Subtiers or Series Limit Type Tier Expression Notes Examples Convergence Two examples Super Large an = n" N/A among many an = n! тп 3" Larger |q|, Exponentially Large An = q", |q| > 1 en larger tier (-2)" (3/2)" nº lim an = ∞ ±an n2 Positive n=1 Larger s, larger tier an = n°, п Power Diverges Vn n'/3 [In(n)]² In(n) Positive Logarithmic Power an = [In(n)]*, s > 0 Larger s, larger tier [In(n)]}/2 Both an and 1/an are bounded 2n Bounded e.g. an — C #0, ап — (-1)", аn %3D n+1 Negative Logarithmic Power In(n)]-1/2 1/ In(n) [In(n)]-2 1/Vn An = [In(n)]ª, Larger s, larger tier ±an n=1 Diverges Or Converges Conditionally" n-1 Negative Power Larger s, larger tier an =n°, Twilight Realm -1.0000001 n-2 lim an = 0 (1/2)" e-n Exponentially Small An = q", 0 < [q| < 1 Larger |q|, larger tier an 1/(-3)" n=1 Converges Absolutely Two examples an = e" /n! Super Small N/A among many An =n-n Zero An = 0 Smallest (2) With the help of the "tierlist", sort the following sequences in descending order: In dn fn en ba Сп e" - (-4)" | т'" | sin(-n) + (-1)" ап n° е—п n2 +n-" (-1)" + 3/In(n) п—е

Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
See similar textbooks
icon
Related questions
Question
Subtiers or Series Limit Type Tier Expression Notes Examples Convergence Two examples Super Large an = n" N/A among many an = n! тп 3" Larger |q|, Exponentially Large An = q", |q| > 1 en larger tier (-2)" (3/2)" nº lim an = ∞ ±an n2 Positive n=1 Larger s, larger tier an = n°, п Power Diverges Vn n'/3 [In(n)]² In(n) Positive Logarithmic Power an = [In(n)]*, s > 0 Larger s, larger tier [In(n)]}/2 Both an and 1/an are bounded 2n Bounded e.g. an — C #0, ап — (-1)", аn %3D n+1 Negative Logarithmic Power In(n)]-1/2 1/ In(n) [In(n)]-2 1/Vn An = [In(n)]ª, Larger s, larger tier ±an n=1 Diverges Or Converges Conditionally" n-1 Negative Power Larger s, larger tier an =n°, Twilight Realm -1.0000001 n-2 lim an = 0 (1/2)" e-n Exponentially Small An = q", 0 < [q| < 1 Larger |q|, larger tier an 1/(-3)" n=1 Converges Absolutely Two examples an = e" /n! Super Small N/A among many An =n-n Zero An = 0 Smallest
Transcribed Image Text:Subtiers or Series Limit Type Tier Expression Notes Examples Convergence Two examples Super Large an = n" N/A among many an = n! тп 3" Larger |q|, Exponentially Large An = q", |q| > 1 en larger tier (-2)" (3/2)" nº lim an = ∞ ±an n2 Positive n=1 Larger s, larger tier an = n°, п Power Diverges Vn n'/3 [In(n)]² In(n) Positive Logarithmic Power an = [In(n)]*, s > 0 Larger s, larger tier [In(n)]}/2 Both an and 1/an are bounded 2n Bounded e.g. an — C #0, ап — (-1)", аn %3D n+1 Negative Logarithmic Power In(n)]-1/2 1/ In(n) [In(n)]-2 1/Vn An = [In(n)]ª, Larger s, larger tier ±an n=1 Diverges Or Converges Conditionally" n-1 Negative Power Larger s, larger tier an =n°, Twilight Realm -1.0000001 n-2 lim an = 0 (1/2)" e-n Exponentially Small An = q", 0 < [q| < 1 Larger |q|, larger tier an 1/(-3)" n=1 Converges Absolutely Two examples an = e" /n! Super Small N/A among many An =n-n Zero An = 0 Smallest
(2) With the help of the "tierlist", sort the following sequences in descending order: In dn fn en ba Сп e" - (-4)" | т'" | sin(-n) + (-1)" ап n° е—п n2 +n-" (-1)" + 3/In(n) п—е
Transcribed Image Text:(2) With the help of the "tierlist", sort the following sequences in descending order: In dn fn en ba Сп e" - (-4)" | т'" | sin(-n) + (-1)" ап n° е—п n2 +n-" (-1)" + 3/In(n) п—е
Expert Solution
Solution:

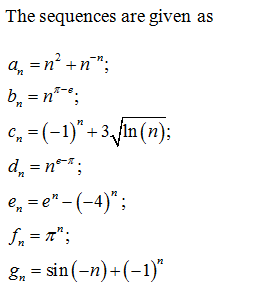
Advanced Math homework question answer, step 1, image 1

Explanation:

Advanced Math homework question answer, step 2, image 1

steps

Step by step

Solved in 3 steps with 3 images

Blurred answer
Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
Basic Technical Mathematics
Basic Technical Mathematics
Advanced Math
ISBN:
9780134437705
Author:
Washington
Publisher:
PEARSON
Topology
Topology
Advanced Math
ISBN:
9780134689517
Author:
Munkres, James R.
Publisher:
Pearson,
SEE MORE TEXTBOOKS