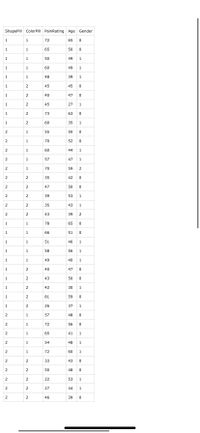
Study 3: Age & Pain. Using the same data set PillShapeColor - use Pearson Correlation and simple linear Regression to create results and then summarize these in APA-style. Run a Pearson Correlation on age and pain rating. Create a scatterplot with pain rating on Y and age on X axis. Run a simple linear regression model with pain rating as DV and age as IV. Regression → Linear Regression, choose your DV, IV(s) –use defaults settings. 1-What is the equation for the regression line? How much variance in pain is accounted for by age (R2)? Interpret this in context of the study (is this a lot of variance explained or not much). 2-Describe the regression results simply and clearly- include the slope and constant and describe what the slope means.  Is age a significant predictor of perceived pain?  Finally, describe what the model predicts about the pain rating of a person who is 40 years old and someone 70 years old.

What is the coefficient of determination in linear regression and how is it interpreted in terms of the strength and quality of the relationship between variables?

The owner of Showtime Movie Theaters, Inc., used multiple regression analysis to predict gross revenue (y) as a function of television advertising (x 1) and newspaper advertising (x 2). The estimated regression equation was ŷ = 87.2 + 1.39 x 1 + 0.54 x 2 Weekly Gross Revenue ($1000s) Televison Advertising ($1000s) Newspaper Advertising ($1000s) 97 6 2.5 91 2 2 96 5 2.5 93 2.5 3.5 95 4 4.3 94 4.5 2.3 94 3.5 4.2 94 4 2.5 The computer solution provided SST = 23.5 and SSR = 22.437. Compute R 2 and R a 2 (to 3 decimals). R 2   R a 2

Categorical binary , categorical ,  or quantataive

please pay attention. you guys have been getting all my stats questions wrong.

Suppose you ran the following regression and found this statistically significant result:   AGE = 120 + -4*HEALTH where AGE is how old someone is and HEALTH is a rating on how healthy they are, from 1 (very unhealthy) to 20 (very healthy). You realize you have it backwards: age causes health, not health causes age. What should the new equation be? 1   HEALTH = -30 + -0.25*AGE 2   It is impossible to tell without re-running the regression. 3   HEALTH = 120 + -4*AGE 4   HEALTH = -30 + 0.25*AGE 5   HEALTH = 30 + -0.25*AGE

The data below is the amount of tar and nicotine in a sample of different brands of 100 mm, non-menthol, filtered cigarettes. a) Using the calculator, find a linear regression model that gives the amount of nicotine, N, as a function of the amount of tar, t. Write the function below. N(t)= b) use this model of nicotine to estimate the amount of nicotine in a cigarette if the amount of tar is listed as 21 mg. c) What is the correlation coefficient, r, for this model? r= Tar 5 16 17 13 13 14 9 15 2 15 13 14 15 16 7 17 Nicotine  0.4 1 1.2 0.8 0.8 1 0.8 1 0.2 1.1 0.8 1 0.9 1.1 0.6 1.3

The data show the chest size and weight of several bears. Find the regression equation, letting chest size be the independent (x) variable. Then find the best predicted weight of a bear with a chest size of 63 inches. Is the result close to the actual weight of 462 pounds? Use a significance level of 0.05. Chest size (inches) Weight (pounds) 58 50 65 59 59 48 414 312 499 450 456 260 Click the icon to view the critical values of the Pearson correlation coefficient r. What is the regression equation? y =+x (Round to one decimal place as needed.) What is the best predicted weight of a bear with a chest size of 63 inches? The best predicted weight for a bear with a chest size of 63 inches is pounds. (Round to one decimal place as needed.) Is the result close to the actual weight of 462 pounds? O A. This result is very close to the actual weight of the bear. O B. This result is close to the actual weight of the bear. O C. This result is not very close to the actual weight of the bear. O D.…

in a regression analysis 68% of students test score is determined by class absenteeism. The relationship between class absenteeism and test score has a linear equation of Y= 34-0.85(X) what the correlation coefficient is a. 0.4624 b. -0.85 c. -0.8246 d none of the above e.0.68

The scatterplot below shows Olympic gold medal performances in the long jump from 1900 to 1988. The long jump is measured in meters. The regression equation is - predicted long jump = 7.24 + 0.014(year since 1900) Describe the association. A. The scatterplot is nonlinear because there is too much variation in the data. B. There is a strong negative association between the amount of protein and the amount of fat that people consume. C. The scatterplot shows a curve. D. This scatterplot shows a moderately strong, positive, linear association between the years since 1990 and the distance of the long jump.