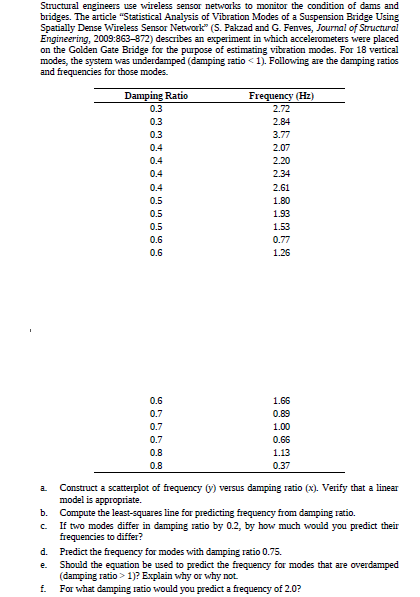
Structural engineers use wireless sensor networks to monitor the condition of dams and bridges. The article "Statistical Analysis of Vibration Modes of a Suspension Bridge Using Spatially Dense Wireless Sensor Network" (S. Pakzad and G. Fenves, Journal of Structural Engineering, 2009:863-872) desaribes an experiment in which accelerometers were placed on the Golden Gate Bridge for the purpose of estimating vibration modes. For 18 vertical modes, the system was underdamped (damping ratio < 1). Following are the damping ratios and frequencies for those modes. Damping Ratio Frequency (Hz) 0.3 2.72 0.3 2.84 0.3 3.77 0.4 2.07 0.4 2.20 0.4 2.34 0.4 2.61 0.5 1.80 0.5 1.93 0.5 1.53 0.6 0.77 0.6 1.26 0.6 1.66 0.7 0.89 0.7 1.00 0.7 0.66 0.8 1.13 0.8 0.37 Construct a scatterplot of frequency ) versus damping ratio (x). Verify that a linear model is appropriate. b. Compute the least-squares line for predicting frequency from damping ratio. If two modes differ in damping ratio by 0.2, by how much would you predict their frequencies to differ? C. d. Predict the frequency for modes with damping ratio 0.75. Should the equation be used to predict the frequency for modes that are overdamped (damping ratio > 1)? Explain why or why not f. e. For what damping ratio would you predict a frequency of 2.0?

The following box plot represents a sample of house prices.

A process engineer is trying to improve the life of a cutting tool. He has run a 2³ experiment using cutting speed (A), metal hardness (B), and cutting angle (C) as the factors. The data from two replicates are shown in Table 13E.2. (1) Calculate the main effects of A, B, C, and all interaction effects. (2) Do any of the three factors affect tool life? Make an ANOVA table and draw conclusion from the F-values with α = 0.05. (3) What combination of factor levels produces the longest tool life? ■ TABLE 13E.2 Data for the Experiment in Exercise 13.2. Replicate Run I II (1) 221 311 a 325 435 b 354 348 ab 552 472 с 440 453 སྣ་ ནྟི 406 377 bc 605 500 abc 392 419

The decline of salmon fisheries along the Columbia River in Oregon has caused great concern among commercial and recreational fishermen. The paper 'Feeding of Predaceous Fishes on Out-Migrating Juvenile Salmonids in John Day Reservoir, Columbia River' (Trans. Amer. Fisheries Soc. (1991: 405-420) gave the accompanying data on y = maximum size of salmonids consumed by a northern squaw fish (the most abundant salmonid predator) and x = squawfish length, both in mm. Here is the computer software printout of the summary: Coefficients:                         Estimate     Std. Error     t value     Pr(> |t|)   (Intercept)   −89.010     16.703     −5.329     0.000   Length   0.705     0.046     15.293     0.000   Using this information, give the equation of the least squares regression line.

Case scenario: A cohort study involved an assessment of the relationship between cigarette smoking and incuof lung cancer. For cigarette smokers, the lung cancer incidence rate was Iexp = 200 per 100,000. For nonsmokers, the lung cancer incidence rate was Iunexp = 25 per 100,000. The lung cancer incidence rate in the entire population was Itotal = 100 per 100,000.  A) what is the relative risk (risk ratio) of developing lung cancer? Interpret this value in plain language?  B) calculate the attributable risk and interpret this value in plain language?  C) calculate the attributable-risk percent and interpret this value in plain language? D) is cigarette smoking a risk factor for lung cancer? Explain your answer. E) Hypothetically speaking, if cigarette smoking could be eliminated from this population, what percentage of lung cancer could be avoided?

NW 6.12 CORPORATE SUSTAINABILITY OF CPA FIRMS. Corporate sustainability refers to business practices designed CORSUS around social and environmental considerations. Refer to the Business and Society (March 2011) study on the sustainability behaviors of CPA corporations, Exercise 2.23 (p. 59). Recall that the level of support for corporate sustainability (measured on a quantitative scale ranging from 0 to 160 points) was obtained for each in a sample of 992 senior managers at CPA firms. Higher point values indicate a higher level of support for sustainability. The accompanying StatCrunch printout gives a 99% confidence interval for the mean level of support for all senior managers at CPA firms. One sample T confidence interval: μ: Mean of variable 99% confidence interval results: Variable Sample Mean Std. Err. DF L. Limit U. Limit Support 67.75504 0.85314633 991 65.553241 69.95684 a. Locate the 99% confidence interval on the printout. b. Use the sample mean and standard deviation on the…

The authors of the paper "Statistical Methods for Assessing Agreement Between Two Methods of Clinical Measurement"† compared two different instruments for measuring a person's ability to breathe out air. (This measurement is helpful in diagnosing various lung disorders.) The two instruments considered were a Wright peak flow meter and a mini-Wright peak flow meter. Seventeen people participated in the study, and for each person air flow was measured once using the Wright meter and once using the mini-Wright meter.   Subject Mini-WrightMeter WrightMeter Subject Mini-WrightMeter WrightMeter 1 512 494 10 445 433 2 430 395 11 432 417 3 520 516 12 626 656 4 428 434 13 260 267 5 500 476 14 477 478 6 600 557 15 259 178 7 364 413 16 350 423 8 380 442 17 451 427 9 658 650         (a) Suppose that the Wright meter is considered to provide a better measure of air flow, but the mini-Wright meter is easier to transport and to use. If the two types of meters produce…