Step 4 To find (f-l)'(x) use the theorem that states that if f is differentiable on an interval I and f has an inverse 1 function g, that is g = f-1, then g is differentiable at any x for which f '(g(x)) ± 0 and g'(x) %3D f'(g(x))' Find the values of f-1(121) and then f'(f-1(121)), f-1(x) = (x + 4)1/3 %3D f-1(121) %3D f'(F-1(121)) = f'I 15 = 31 15 75 75 %3D Step 5 1 Substitute the above values in the expression for (f-1)'(121): f'(F=1(121))" 1 (F-1)'(121) = f'(F=1(121)) 1 75 Thus, (f-1)'(121) = 5
Step 4 To find (f-l)'(x) use the theorem that states that if f is differentiable on an interval I and f has an inverse 1 function g, that is g = f-1, then g is differentiable at any x for which f '(g(x)) ± 0 and g'(x) %3D f'(g(x))' Find the values of f-1(121) and then f'(f-1(121)), f-1(x) = (x + 4)1/3 %3D f-1(121) %3D f'(F-1(121)) = f'I 15 = 31 15 75 75 %3D Step 5 1 Substitute the above values in the expression for (f-1)'(121): f'(F=1(121))" 1 (F-1)'(121) = f'(F=1(121)) 1 75 Thus, (f-1)'(121) = 5
Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
100%
![**Step 4**
To find \((f^{-1})'(x)\), use the theorem that states that if \(f\) is differentiable on an interval \(I\) and \(f\) has an inverse function \(g\), that is \(g = f^{-1}\), then \(g\) is differentiable at any \(x\) for which \(f'(g(x)) \neq 0\) and \(g'(x) = \frac{1}{f'(g(x))}\).
Find the values of \(f^{-1}(121)\) and then \(f'(f^{-1}(121))\),
\[ f^{-1}(x) = (x + 4)^{1/3} \]
\[ f^{-1}(121) = 5 \]
\[ f'(f^{-1}(121)) = f'(5) \]
\[ = 3(5)^2 \]
\[ = 75 \]
**Step 5**
Substitute the above values in the expression for \((f^{-1})'(121) = \frac{1}{f'(f^{-1}(121))}\).
\[ (f^{-1})'(121) = \frac{1}{75} \]
Thus, \((f^{-1})'(121) = \frac{1}{75}\).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F679cf9fe-7ea4-4759-a28d-7fe07c30cdca%2F36d90f50-e676-43a0-94f0-f87f7a03b138%2F8ikavd_processed.png&w=3840&q=75)
Transcribed Image Text:**Step 4**
To find \((f^{-1})'(x)\), use the theorem that states that if \(f\) is differentiable on an interval \(I\) and \(f\) has an inverse function \(g\), that is \(g = f^{-1}\), then \(g\) is differentiable at any \(x\) for which \(f'(g(x)) \neq 0\) and \(g'(x) = \frac{1}{f'(g(x))}\).
Find the values of \(f^{-1}(121)\) and then \(f'(f^{-1}(121))\),
\[ f^{-1}(x) = (x + 4)^{1/3} \]
\[ f^{-1}(121) = 5 \]
\[ f'(f^{-1}(121)) = f'(5) \]
\[ = 3(5)^2 \]
\[ = 75 \]
**Step 5**
Substitute the above values in the expression for \((f^{-1})'(121) = \frac{1}{f'(f^{-1}(121))}\).
\[ (f^{-1})'(121) = \frac{1}{75} \]
Thus, \((f^{-1})'(121) = \frac{1}{75}\).
Expert Solution
Step 1
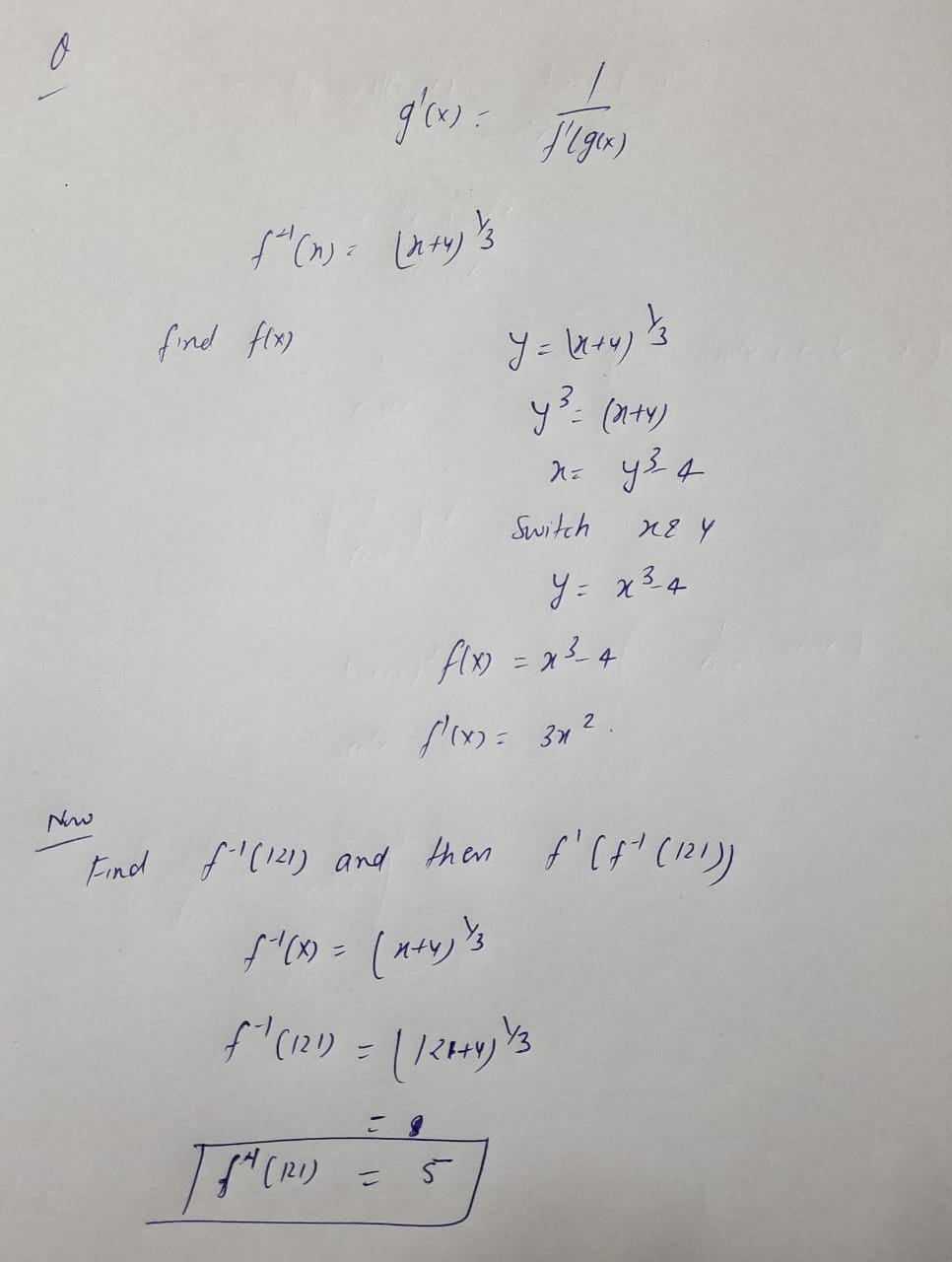
Step by step
Solved in 2 steps with 2 images
Recommended textbooks for you
Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning