Standard Normal Curve Areas (page 1) The column under A gives the proportion of the area under the entire curve that is between z= 0 and a positive value of z. Z A z 0.00 0.000 0.30 0.01 0.004 0.31 0.02 0.008 0.32 0.126 0.62 0.129 0.63 0.64 0.133 0.137 0.65 0.141 0.245 0.66 0.67 0.249 0.68 0.03 0.012 0.33 0.04 0.016 0.34 0.05 0.020 0.35 0.06 0.024 0.36 0.07 0.028 0.37 0.144 0.08 0.032 0.38 0.148 0.09 0.036 0.39 0.152 0.69 0.10 0.040 0.40 0.11 0.044 0.41 0.12 0.048 0.42 0.13 0.052 0.43 0.14 0.056 0.44 0.15 0.060 0.45 0.064 0.46 0.067 0.47 0.16 0.17 A 0.118 0.122 0.18 0.071 0.19 0.075 Areas under the Normal Curve s 0 2 A z A z 0.226 0.90 0.316 1.20 0.229 0.91 0.319 1.21 0.232 0.92 0.321 1.22 0.236 1.23 1.24 0.393 1.54 0.93 0.324 0.239 0.94 0.326 0.242 0.95 1.55 0.329 1.25 0.394 0.331 1.26 0.334 1.27 0.252 0.98 0.336 1.28 1.29 0.255 0.99 0.258 1.00 1.01 0.344 0.339 0.341 0.261 0.264 1.02 0.346 0.348 0.267 1.03 0.20 0.079 0.21 0.083 0.22 0.087 0.52 0.23 0.091 0.53 0.095 0.24 0.25 0.099 0.26 0.103 0.106 0.57 0.216 0.110 0.58 0.219 0.114 0.59 0.222 Z 0.60 0.61 0.155 0.159 0.163 0.72 0.166 0.73 0.198 0.202 0.70 0.71 0.170 0.174 0.177 0.181 0.48 0.184 0.78 0.282 0.49 0.188 0.79 0.50 0.191 0.80 0.51 0.195 0.81 0.74 0.75 0.76 0.77 0.82 0.83 0.205 0.84 0.54 0.55 0.209 0.212 0.56 0.270 1.04 0.273 1.05 0.96 0.97 0.276 1.06 0.279 1.07 1.08 0.360 1.38 1.09 0.362 1.39 1.10 0.364 1.11 0.367 0.294 1.12 0.297 1.13 0.300 1.14 0.85 0.302 1.15 0.86 0.305 1.16 0.87 0.308 1.17 0.88 0.311 1.18 0.89 0.313 1.19 The column under A gives the proportion of the area under the entire curve that is between z= 0 and a positive value of z. 0.285 0.288 0.291 0.27 0.28 0.29 Standard Normal Curve Areas (page 2) Because the curve is symmetric about 0, the area between z=0 and a negative value of z can be found by using the corresponding positive value of z. 0.351 1.34 0.353 1.35 0.355 1.36 0.358 1.37 Areas under the Normal Curve 1.30 0.403 1.31 0.405 1.32 0.407 1.62 1.33 0.408 1.63 0.410 1.64 0.411 1.65 0.413 1.66 0.415 1.67 A z A 0.385 1.50 0.433 0.387 1.51 0.434 0.389 1.52 0.391 1.53 1.48 1.49 0.396 1.56 0.441 0.398 1.57 0.442 0.400 1.58 0.443 0.401 1.59 0.444 1.60 0.445 1.61 0.446 0.447 0.448 0.449 0.451 1.40 0.419 1.41 0.421 1.71 0.369 1.42 1.72 0.371 1.43 1.73 0.373 1.44 0.425 1.74 0.375 1.45 0.426 1.75 0.377 1.46 0.428 1.76 0.379 1.47 0.429 1.77 0.381 0.383 0.416 1.68 0.418 1.69 1.70 0.422 0.424 0.431 0.432 0.436 0.437 0.438 0.439 1.78 1.79 0.452 0.453 0.454 0.454 0.455 0.456 0.457 0.458 0.459 0.460 0.461 0.462 0.462 0.463 Because the curve is symmetric about 0, the area between z=0 and a negative value of z can be found by using the corresponding positive value of z.
Standard Normal Curve Areas (page 1) The column under A gives the proportion of the area under the entire curve that is between z= 0 and a positive value of z. Z A z 0.00 0.000 0.30 0.01 0.004 0.31 0.02 0.008 0.32 0.126 0.62 0.129 0.63 0.64 0.133 0.137 0.65 0.141 0.245 0.66 0.67 0.249 0.68 0.03 0.012 0.33 0.04 0.016 0.34 0.05 0.020 0.35 0.06 0.024 0.36 0.07 0.028 0.37 0.144 0.08 0.032 0.38 0.148 0.09 0.036 0.39 0.152 0.69 0.10 0.040 0.40 0.11 0.044 0.41 0.12 0.048 0.42 0.13 0.052 0.43 0.14 0.056 0.44 0.15 0.060 0.45 0.064 0.46 0.067 0.47 0.16 0.17 A 0.118 0.122 0.18 0.071 0.19 0.075 Areas under the Normal Curve s 0 2 A z A z 0.226 0.90 0.316 1.20 0.229 0.91 0.319 1.21 0.232 0.92 0.321 1.22 0.236 1.23 1.24 0.393 1.54 0.93 0.324 0.239 0.94 0.326 0.242 0.95 1.55 0.329 1.25 0.394 0.331 1.26 0.334 1.27 0.252 0.98 0.336 1.28 1.29 0.255 0.99 0.258 1.00 1.01 0.344 0.339 0.341 0.261 0.264 1.02 0.346 0.348 0.267 1.03 0.20 0.079 0.21 0.083 0.22 0.087 0.52 0.23 0.091 0.53 0.095 0.24 0.25 0.099 0.26 0.103 0.106 0.57 0.216 0.110 0.58 0.219 0.114 0.59 0.222 Z 0.60 0.61 0.155 0.159 0.163 0.72 0.166 0.73 0.198 0.202 0.70 0.71 0.170 0.174 0.177 0.181 0.48 0.184 0.78 0.282 0.49 0.188 0.79 0.50 0.191 0.80 0.51 0.195 0.81 0.74 0.75 0.76 0.77 0.82 0.83 0.205 0.84 0.54 0.55 0.209 0.212 0.56 0.270 1.04 0.273 1.05 0.96 0.97 0.276 1.06 0.279 1.07 1.08 0.360 1.38 1.09 0.362 1.39 1.10 0.364 1.11 0.367 0.294 1.12 0.297 1.13 0.300 1.14 0.85 0.302 1.15 0.86 0.305 1.16 0.87 0.308 1.17 0.88 0.311 1.18 0.89 0.313 1.19 The column under A gives the proportion of the area under the entire curve that is between z= 0 and a positive value of z. 0.285 0.288 0.291 0.27 0.28 0.29 Standard Normal Curve Areas (page 2) Because the curve is symmetric about 0, the area between z=0 and a negative value of z can be found by using the corresponding positive value of z. 0.351 1.34 0.353 1.35 0.355 1.36 0.358 1.37 Areas under the Normal Curve 1.30 0.403 1.31 0.405 1.32 0.407 1.62 1.33 0.408 1.63 0.410 1.64 0.411 1.65 0.413 1.66 0.415 1.67 A z A 0.385 1.50 0.433 0.387 1.51 0.434 0.389 1.52 0.391 1.53 1.48 1.49 0.396 1.56 0.441 0.398 1.57 0.442 0.400 1.58 0.443 0.401 1.59 0.444 1.60 0.445 1.61 0.446 0.447 0.448 0.449 0.451 1.40 0.419 1.41 0.421 1.71 0.369 1.42 1.72 0.371 1.43 1.73 0.373 1.44 0.425 1.74 0.375 1.45 0.426 1.75 0.377 1.46 0.428 1.76 0.379 1.47 0.429 1.77 0.381 0.383 0.416 1.68 0.418 1.69 1.70 0.422 0.424 0.431 0.432 0.436 0.437 0.438 0.439 1.78 1.79 0.452 0.453 0.454 0.454 0.455 0.456 0.457 0.458 0.459 0.460 0.461 0.462 0.462 0.463 Because the curve is symmetric about 0, the area between z=0 and a negative value of z can be found by using the corresponding positive value of z.
Glencoe Algebra 1, Student Edition, 9780079039897, 0079039898, 2018
18th Edition
ISBN:9780079039897
Author:Carter
Publisher:Carter
Chapter10: Statistics
Section10.5: Comparing Sets Of Data
Problem 13PPS
Related questions
Question
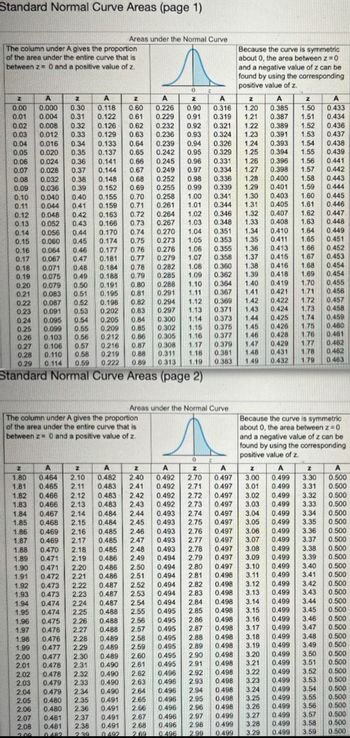
Transcribed Image Text:Standard Normal Curve Areas (page 1)
The column under A gives the proportion
of the area under the entire curve that is
between z= 0 and a positive value of z.
A
z
A
z
A
0.60 0.226
0.122 0.61 0.229
z
0.00 0.000 0.30 0.118
0.01 0.004 0.31
0.02 0.008 0.32 0.126 0.62 0.232 0.92
0.03 0.012 0.33 0.129 0.63 0.236 0.93
0.04 0.016 0.34 0.133 0.64 0.239
0.05 0.020 0.35 0.137 0.65
0.06 0.024 0.36 0.141 0.66
0.07 0.028 0.37 0.144 0.67
0.08 0.032 0.38 0.148 0.68
0.94
0.242
0.95
0.245
0.96
0.249 0.97
0.09 0.036 0.39 0.152 0.69
0.10 0.040 0.40 0.155 0.70 0.258
0.11 0.044 0.41 0.159 0.71 0.261
0.12 0.048 0.42 0.163 0.72 0.264
0.13 0.052 0.43 0.166 0.73 0.267
0.270
0.14 0.056 0.44
0.060
0.15
0.45
0.273
0.16 0.064
0.067
0.071
0.075
0.17
0.18
0.19
0.26 0.103
0.27
0.48
0.49
0.20 0.079 0.50
0.21
0.083
0.52
0.087
0.22
0.23 0.091 0.53
0.24
0.25 0.099
0.095 0.54
0.55
1.94
1.95
1.96
1.97
1.98
1.99
2.00
0.46
0.47
0.198
0.202
0.205
0.209
0.56 0.212
0.106 0.57
0.216
0.110 0.58 0.219
0.222
0.59
2.05
2.06
0.170
0.174
Areas under the Normal Curve
s
0
z
z
0.475
0.476
0.476
0.477
0.477
0.478
0.177
0.181
0.184
0.188
0.191
0.51 0.195 0.81
The column under A gives the proportion
of the area under the entire curve that is
between z= 0 and a positive value of z.
2.01
2.02
2.03
2.04 0.479
0.480
0.480 2.36
2.37
2.38
2.39
0.478
0.479
0.74
0.75
2.07
0.481
2.08 0.481
2.00 0.482
0.82
0.83
0.84
0.85
0.86
0.87
0.88
0.89
0.76
0.276
1.06
0.77
0.279 1.07
0.78
0.282
0.79 0.285
0.80 0.288
0.291
0.28
0.29 0.114
Standard Normal Curve Areas (page 2)
0.252 0.98
0.255 0.99
1.00
1.01
0.294
0.297
0.90
0.91
2.61
2.62
2.63
0.490
0.490
2.33
2.64
2.34 0.490
0.491
2.35
2.65
0.491
2.66
0.491 2.67
0.491
2.68
0.492
2.69
1.02
1.03
1.08
1.09
0.496
0.496
0.496
1.10
1.11
0.300
0.302
0.305
0.308
1.17
0.311 1.18
0.313 1.19
0.496
0.496
1.12
1.13
1.14
1.15
1.16
A
0.316
0.319
0.321
0.324
0.341 1.30
0.403 1.60
0.344 1.31 0.405 1.61
0.346 1.32
0.348 1.33
1.04
0.351
1.05 0.353
Areas under the Normal Curve
0
Z
z
A
Z
A
Z
Z
2.73 0.497
A
A
1.80 0.464 2.10 0.482
2.40 0.492 2.70 0.497 3.00
1.81 0.465 2.11 0.483 2.41 0.492 2.71 0.497 3.01
1.82 0.466 2.12 0.483 2.42 0.492
2.72 0.497
1.83 0.466 2.13 0.483
2.43
0.492
1.84 0.467 2.14 0.484 2.44 0.493 2.74 0.497
1.85 0.468 2.15 0.484 2.45 0.493 2.75 0.497
1.86 0.469 2.16 0.485 2.46 0.493 2.76 0.497 3.06
1.87 0.469 2.17 0.485 2.47 0.493 2.77 0.497 3.07
0.485 2.48 0.493
1.89 0.471 2.19 0.486 2.49 0.494
1.88 0.470 2.18
1.90 0.471 2.20
1.91
1.92
2.22
0.473
1.93 0.473 2.23
0.474
0.474
0.355
0.358
Because the curve is symmetric
about 0, the area between z=0
and a negative value of z can be
found by using the corresponding
positive value of z.
2
0.496
0.496
0.496 2.99
z
1.20
1.21
1.22
1.23
0.326
0.329
0.331 1.26 0.396 1.56
0.334 1.27
0.398
1.57
0.336 1.28
0.400 1.58
0.339 1.29
0.401 1.59
0.389
1.52
0.391 1.53
1.24
0.393
1.25 0.394
1.66
1.67
1.68
1.69
0.364
1.70
0.367
0.421 1.71
0.369
0.422 1.72
0.371
0.424
1.73
0.373 1.44 0.425
1.74
0.375
1.45
0.426
0.377 1.46
0.428
0.379
0.429 1.77
0.381
0.431
1.78
0.383
0.432 1.79
1.36
1.37
2.80
0.486 2.50 0.494
0.472 2.21 0.486
2.51 0.494 2.81
0.487 2.52 0.494 2.82 0.498 3.12 0.499
0.487 2.53 0.494 2.83 0.498
2.84 0.498
0.495 2.85 0.498
0.487
2.24
3.13 0.499
3.14 0.499
3.15 0.499
2.54 0.494
2.55
2.56
2.25 0.488
2.26
0.488
0.495 2.86
0.498
2.27
0.488
2.57
0.495
2.87
0.498
2.28
0.489
2.58
0.495
2.88
0.498
2.29
0.489
2.59
0.495 2.89
0.498
2.30
0.489
2.60
0.495 2.90
2.31
0.490
0.495
2.91
2.32
2.92
2.93
2.94
2.95
2.97 0.499
2.98 0.499
0.499
A
z
0.385 1.50
0.387 1.51
0.360 1.38
0.362
1.39
0.419
1.40
1.41
1.42
1.43
1.47
1.48
1.49
0.407 1.62 0.447
0.408 1.63
1.34 0.410 1.64
1.35 0.411
1.65
0.413
0.415
3.16
3.17
0.416
0.418
0.498
0.498
3.22
0.498
3.23
0.498
3.24
0.498 3.25
3.26
3.27
3.28
3.29
0.498
2.96
1.54
1.55
3.20
0.498
3.21
Because the curve is symmetric
about 0, the area between z=0
and a negative value of z can be
found by using the corresponding
positive value of z.
Z
A
0.499 3.30
0.499 3.31
3.32
3.33
1.75
1.76
3.02 0.499
3.03 0.499
3.04 0.499 3.34 0.500
3.05 0.499 3.35
0.500
0.500
0.500
0.499 3.36
0.499 3.37
2.78 0.497 3.08 0.499
3.38
0.500
3.09 0.499 3.39 0.500
2.79
0.497
0.497 3.10 0.499 3.40 0.500
0.498 3.11 0.499 3.41
0.500
3.42
0.500
3.43
0.500
3.44
0.500
3.45
0.500
0.499 3.46
0.500
0.499 3.47
0.500
3.18
0.499
3.48
3.19 0.499 3.49
0.499
3.50
0.499
3.51
0.499
3.52
0.499
A
0.433
0.434
0.436
0.437
0.438
0.439
0.441
0.442
0.443
0.444
0.499
0.499
0.499
0.445
0.446
0.499 3.54
0.448
0.449
0.451
0.452
0.453
0.454
0.454
0.455
0.456
0.457
0.458
0.459
0.460
0.461
0.462
0.462
0.463
A
0.500
0.500
0.500
0.500
0.500
0.500
0.500
0.500
0.500
3.53 0.500
0.500
0.500
0.500
3.55
0.499
0.499
3.56
3.57
3.58
3.59
0.500
0.500
0.500
Transcribed Image Text:In nutrition, the recommended daily allowance of vitamins is a number set by the government to guide an individual's daily vitamin intake. Actually, vitamin needs vary drastically from person
to person, but the needs are closely approximated by a normal curve. To calculate the recommended daily allowance, the government first finds the standard deviation and the average need for
vitamins among people in the population. The recommended daily allowance is then defined as the mean plus 2.4 times the standard deviation. What fraction of the population will receive adequate
amounts of vitamins under this plan?
Click here to see page 1 of the table for areas under the standard normal curve.
Click here to see page 2 of the table for areas under the standard normal curve
CID
The fraction of the population that will receive adequate amounts of vitamins under the given plan is
(Type an integer or decimal rounded to the nearest thousandth as needed.).
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 2 images
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897…
Algebra
ISBN:
9780079039897
Author:
Carter
Publisher:
McGraw Hill
Big Ideas Math A Bridge To Success Algebra 1: Stu…
Algebra
ISBN:
9781680331141
Author:
HOUGHTON MIFFLIN HARCOURT
Publisher:
Houghton Mifflin Harcourt
College Algebra (MindTap Course List)
Algebra
ISBN:
9781305652231
Author:
R. David Gustafson, Jeff Hughes
Publisher:
Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897…
Algebra
ISBN:
9780079039897
Author:
Carter
Publisher:
McGraw Hill
Big Ideas Math A Bridge To Success Algebra 1: Stu…
Algebra
ISBN:
9781680331141
Author:
HOUGHTON MIFFLIN HARCOURT
Publisher:
Houghton Mifflin Harcourt
College Algebra (MindTap Course List)
Algebra
ISBN:
9781305652231
Author:
R. David Gustafson, Jeff Hughes
Publisher:
Cengage Learning