Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Related questions
Question
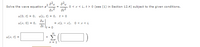
Transcribed Image Text:Solve the wave equation a
2
0 < x< L, t > 0 (see (1) in Section 12.4) subject to the given conditions.
=
u(0, t) = 0, u(L, t) = 0, t> 0
du
u(x, 0) = 0,
= x(L - x), 0<x < L
It = 0
Σ
u(x, t) =
+
n = 1
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 3 images
Knowledge Booster
Similar questions
- Question 97 What does the notion of y(0-) mean in the realm of signals and systems? Choose your answer from the below choices: a) the signal y(t) right before time t = 0 b) the signal y(t) at the moment t = 0 c) the signal y(t) when the input x(t) is 0 d) the signal y for an input frequency slightly below 0 Hzarrow_forward3) Can you answer just a,b,carrow_forwardfrom t=1 to t=2. Hint: perfect square. ""(t)/(Ir'(t) x r''(t) 1)2. Compute a constant. Here x denotes cross da and b are constants. al/first order wave equation Utt=Uxx- f(x,y)=(x²/2)+3y³+9y²-3xy+9y-9x. -3) is Saddle Point (12.1) is local MIN ounded by the lines x=0, x=2, y=x is the region in the first quadrant at the origin. 7) Calculate SSS x²y²z² du where {AL F = {(x₁1₁2) | -1 ≤ x ≤ 1, -147, 51, -1 ≤ 2 ≤₁3arrow_forward
- Q2) Solve the wave equation u=u 00 " XX 11 subject to u(0,t) = u(2,t) =0, t>0 and u(x,0)=0, u )=0, u,(x,0): = sin (3лx), 0arrow_forward2. (Section 17.2) Evaluate point (-2, 0,3π). Lyd y dx − x dy + 3y dz if curve C is the part of (t) = from point (2,0,0) toarrow_forwardO Verify that the u = Cos 4 t sin 2x Solution of Wave Equation with suitable C Verify that the function u- e sin wx is a Solution of the Heat Equation with Suitable c tan ) O Verify that the fanc tion u = is a Solution of the Laplace Eguation.arrow_forwardPlease give me answers in 5min I will give you like surearrow_forwardPlease solve asaparrow_forwardA string with motionless ends at x = 0 and x = 1 vibrates according to the wave equation Fu Ət² and the initial velocity J²u dr² 1. Use separation of variables (show details) to solve the equation provided that the initial profile of the string is u(x,0) = 4 sin(2x) Ju 5- Ət It=0 = 0.arrow_forwardarrow_back_iosarrow_forward_ios
Recommended textbooks for you
- Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY 
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,