
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question

Transcribed Image Text:function f(t)
1
tn
eat
sin at
cos at
sinh at
cosh at
e-at f(t)
U(ta) or Ua(t) (a ≥ 0)
(ta) (a> 0)
U(t − a)f(t − a) or Ua(t)f(t − a)
f(n)(t)
(−t)" f (t)
-
(fg)(t) = f(r)g(t − T) dr
Laplace transform F(s)
1/s
(s > 0)
n!/sn+1 (s > 0)
1/(s – a)
(s> a)
a/(s²+a²) (s > 0)
s/(s² + a²)
(s > 0)
a/(s² - a²)
(s> |a|)
s/(s² – a²)
F(s+a
(s>|a|)
-as
e
S S
0)
as
e
as
e
S
F(s
F(n)(s)
F(s)G(s)
sn
¯¹ƒ (0) — sn−² ƒ'(0) … … … — ƒ (n−¹) (0)
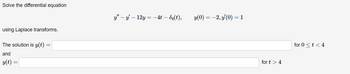
Transcribed Image Text:Solve the differential equation
บ''
"-y-12y=-4-5₁(t), y(0) = −2, y'(0) = 1
using Laplace transforms.
The solution is y(t)
and
y(t):
=
=
fort > 4
for 0 < t <4
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps

Knowledge Booster
Similar questions
- Let f(x)= = 6 sin x 6 sin + 4 cos a Then f'(x) = π The equation of the tangent line to y = f(x) at a = can be written in the form y = mx + b where 2 -m= and b=arrow_forward5 i+ cos' (61)j + lIn (2r³)k. t – 2 Calculate the derivative of the function r(t) = -arrow_forward1. Find f. f ''(?) = sin(?) + cos(?), f(0) = 1, f '(0) = 2 f(?) =arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

