Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
Bartleby Related Questions Icon

Related questions

Q: Solve 4x + 5-9x +15>0
A: To solve  4x + 5-9x +15>0
Q: Solve for 91- = 320-5.
A: Solve by logarithmic
Q: Solve: b-13 = b-13 4 O 13 O-11 O 14 O 15
A:
Q: Solve. 3c9-18c2 81c
A: topic - cubic polynomial
Q: Can you please solve for 5A + 5B
A:
Q: Solve  6-x=2x+9
A:
Q: Find the number of roots for the equation. 5x4 + 12x³ – x² + 3x + 5 = 0
A: As we know that the number of roots is equal to the highest power of the polynomial.
Q: 1. Solve : 5(3**2) = 125
A:
Q: ナ -4-
A:
Q: solve for b a=1\2bh
A: We will find the value of b in terms of a and h as following .
Q: Solve 2x4+36x > 8x3+6x2
A: Given that the inequality is
Q: Solve -5x - 3 =4x + 3
A:
Q: 5х - 4
A: The given question is taken from the inequality in which we have to solve the given inequality we…
Q: solve  (x+2)2=16 x=
A:
Q: Can you help me solve #5
A: Given: function and interval.
Q: solve yiv + 2y" = 0
A:
Question
Solve number 2
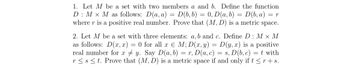
1. Let M be a set with two members a and b. Define the function D: M X M as follows: D(a, a) = D(b, b) 0, D (a, b) D(b, a) = = r where r is a positive real number. Prove that (M, D) is a metric space. = 2. Let M be a set with three elements: a, b and c. Define D: M X M as follows: D(x,x) = 0 for all x E M; D(x, y) = D(y, x) is a positive real number for xy. Say D(a, b) = r, D(a, c) = s, D(b, c) = t with r≤st. Prove that (M, D) is a metric space if and only if t ≤r + s.
expand button
Transcribed Image Text:1. Let M be a set with two members a and b. Define the function D: M X M as follows: D(a, a) = D(b, b) 0, D (a, b) D(b, a) = = r where r is a positive real number. Prove that (M, D) is a metric space. = 2. Let M be a set with three elements: a, b and c. Define D: M X M as follows: D(x,x) = 0 for all x E M; D(x, y) = D(y, x) is a positive real number for xy. Say D(a, b) = r, D(a, c) = s, D(b, c) = t with r≤st. Prove that (M, D) is a metric space if and only if t ≤r + s.
Expert Solution
Check Mark
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
bartleby
This is a popular solution
See solutionCheck out a sample Q&A here
Step 1
VIEW
Step 2
VIEW
bartleby

Trending nowThis is a popular solution!

bartleby

Step by stepSolved in 2 steps with 2 images

See solution
Check out a sample Q&A here
Blurred answer
Knowledge Booster
Background pattern image
Similar questions
Recommended textbooks for you
Text book image
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Text book image
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Text book image
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Text book image
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Text book image
Basic Technical Mathematics
Advanced Math
ISBN:9780134437705
Author:Washington
Publisher:PEARSON
Text book image
Topology
Advanced Math
ISBN:9780134689517
Author:Munkres, James R.
Publisher:Pearson,
SEE MORE TEXTBOOKS