
Concept explainers
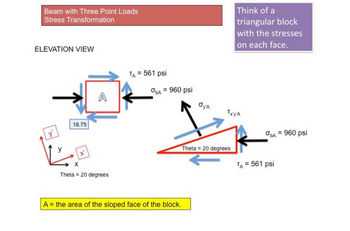
Solve for the equivalent force on an inclined surface. Look at Figure A.1 below. You will see a triangular block cut from a stress block with known stresses. The size and thickness of the block does not matter, so we will assume the area of the sloped inclined surface is A (sorry that it is the same symbol as the Point). If the area of the sloped surface is A, then the area of the other two surfaces is A cos (Theta) and A sin (Theta). First, draw a FBD of the block by multiplying each stress (normal and shear, known and unknown) by their associated area (in terms of A). Second, break the stress
Step by stepSolved in 4 steps with 3 images

- The strain components e, E, and yy are given for a point in a body subjected to plane strain. Using Mohr's circle, determine the principal strains, the maximum in-plane shear strain, and the absolute maximum shear strain at the point. Show the angle 0, the principal strain deformations, and the maximum in-plane shear strain distortion in a sketch. Ex = 390 µe, ɛ, = -630 pe, Vxy = -760 prad. Enter the angle such that -45°s0,s +45°. Answer: Ep1 = Ep2 = Ymax in-plane prad Yabsolute max. prad 0p =arrow_forwardAn element in plane stress is subjected to stresses σ_x, σ_y, and τ_xy (see figure). Using Mohr’s circle, determine the stresses acting on an element oriented at an angle θ from the x axis. Show these stresses on a sketch of an element oriented at the angle θ. (Note: The angle θ is positive when counterclockwise and negative when clockwise.) Given: σ_x=33 MPa,σ_y=-9 MPa,τ_xy=29 MPa,θ=35°arrow_forward

 Structural Analysis (10th Edition)Civil EngineeringISBN:9780134610672Author:Russell C. HibbelerPublisher:PEARSON
Structural Analysis (10th Edition)Civil EngineeringISBN:9780134610672Author:Russell C. HibbelerPublisher:PEARSON Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning
Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning Fundamentals of Structural AnalysisCivil EngineeringISBN:9780073398006Author:Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel LanningPublisher:McGraw-Hill Education
Fundamentals of Structural AnalysisCivil EngineeringISBN:9780073398006Author:Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel LanningPublisher:McGraw-Hill Education
 Traffic and Highway EngineeringCivil EngineeringISBN:9781305156241Author:Garber, Nicholas J.Publisher:Cengage Learning
Traffic and Highway EngineeringCivil EngineeringISBN:9781305156241Author:Garber, Nicholas J.Publisher:Cengage Learning





