Question

Transcribed Image Text:Solid metals can be modeled as a set of uncoupled harmonic oscillators of the same
frequency with energy levels given by
En = ħwn
n = 0, 1, 2,...
where the zero-point energy (the lowest energy state) of each oscillator has been adjusted
to zero for simplicity. In this model, the harmonic oscillators represent the motions of the
metal atoms relative to one another. The frequency of these oscillators is low so that
ħw
= = 224
KB
and the system vibrational partition function is given by
3N
Z
² = la₁ -
(1
1
e-0/T).
(a) If the system contains one mole of atoms, find the average energy (in J) of this system at
T= 172 K. (You can use =
BkB.)
T
(b) What is the absolute entropy (in J/K) for this system? You can use either the Gibbs
expression for S, or the system partition function to make this evaluation (they are
equivalent, as your reading assignment indicates).
Expert Solution
arrow_forward
Step 1
The required solution is following
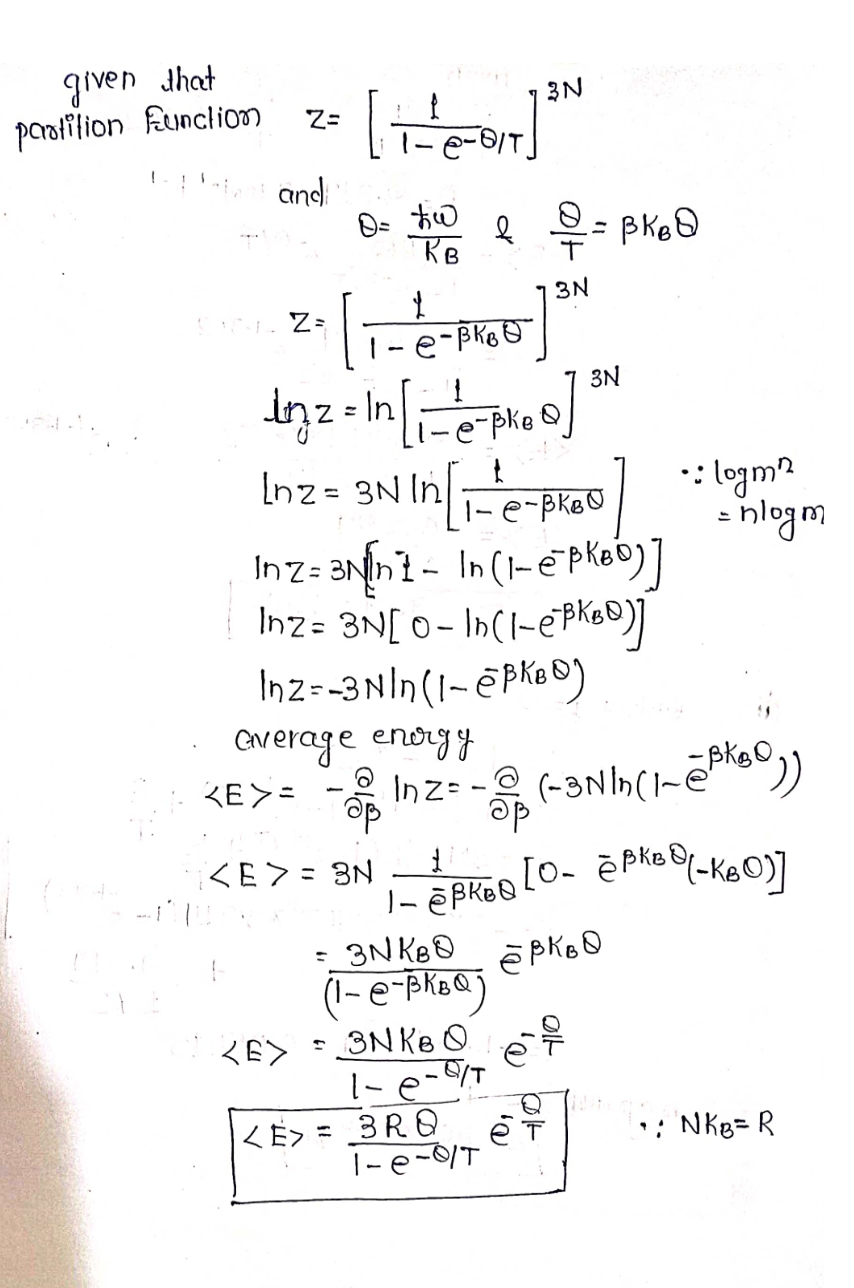
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- A quantum system is described by a wave function (r) being a superposition of two states with different energies E1 and E2: (x) = c191(r)e iEit/h+ c292(x)e¯iE2t/h. where ci = 2icz and the real functions p1(x) and p2(r) have the following properties: vile)dz = ile)dz = 1, "0 = rp(x)T#(x)l& p1(x)92(x)dx% D0. Calculate: 1. Probabilities of measurement of energies E1 and E2 2. Expectation valuc of cnergy (E)arrow_forwardAn electron moving in a box of length ‘a’. If Z1 is the wave function at x1 = a/4 with n=1 and Z2 at x = a/4 for n=2 find Z1/Z2arrow_forwardAn electron is trapped in an infinitely deep one-dimensional well of width 0,251 nm. Initially the electron occupies the n=4 state. Suppose the electron jumps to the ground state with the accompanying emission of photon. What is the energy of the photon?arrow_forward
- A particle is in the n = 9 excited state of a quantum simple harmonic oscillator well. A photon with a frequency of 3.95 x 1015 Hz is emitted as the particle moves to the n = 7 excited state. What is the minimum photon frequency required for this particle to make a quantum jump from the ground state of this well to the n = 8 excited state? (Give your answer in Hz.)arrow_forwardA hypothetical molecule oscillates with a natural frequency of 1.4 × 1013 Hz. Part (a) What is the energy difference, in electron volts, between adjacent harmonic oscillator states of the hypothetical molecule? Part (b) What is the quantum number of the state of the hypothetical molecule that has an energy of 0.75 eV? Round your answer to the nearest integer.arrow_forward
arrow_back_ios
arrow_forward_ios