
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
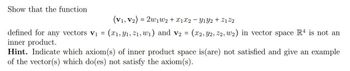
Transcribed Image Text:Show that the function
(V1, V2) = 2w₁ W2 + X1 X2 - Y1Y2 + Z122
defined for any vectors V₁ = (x1, y₁, 2₁,w₁) and v₂ = (x2, Y2, 22, w₂) in vector space R4 is not an
inner product.
Hint. Indicate which axiom(s) of inner product space is (are) not satisfied and give an example
of the vector(s) which do(es) not satisfy the axiom(s).
Expert Solution
arrow_forward
Step 1: Example
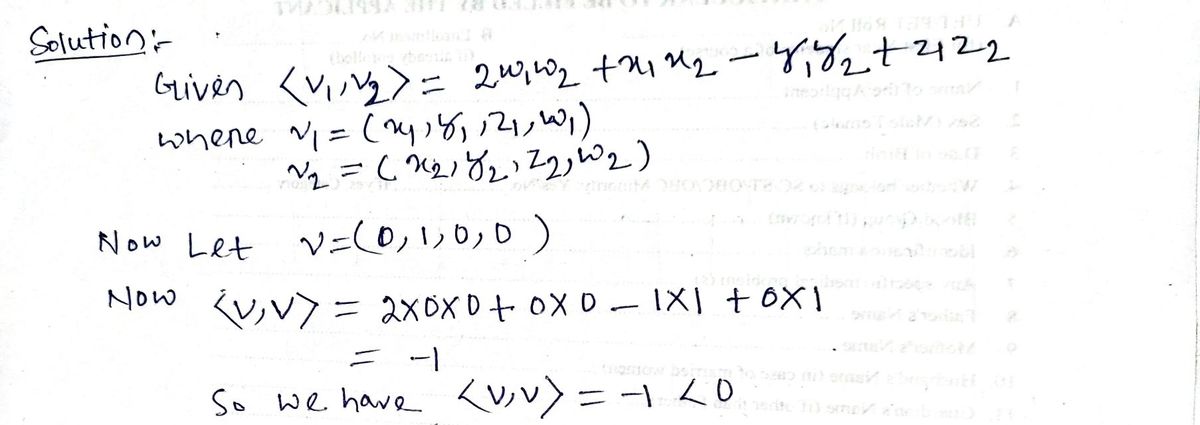
Step by stepSolved in 3 steps with 2 images

Knowledge Booster
Similar questions
- Suppose V1, V2, V3 is an orthogonal set of vectors in R5. Let w be a vector in Span(v1, V2, V3) such that V₁ V₁ = 35, v₂ · V2 = 334, V3 V3 . . = 16, w.v₁ = -105, w. v2 - 2338, w - V3 then w = =v₁+0₂ + v3. : 48, =arrow_forwardLet U be a subspace of R", and let S = { ū, v, w } be a set of three non-zero vectors in R”. Fill in the blanks so that the following statements are true. If you believe you don't have enough information to conclude anything for any of the cases, choose the answer "???". Note that there is no intended relationship between the parts. In each case, assume only what the statement says to assume. If SCU, then dim(U) > (Enter the largest integer that makes the statement necessarily true.) If S is linearly independent and S C U, then dim(U) 3. If S' is a spanning set for U, then dim(U) 3. If span(S) = U then S If S is a basis for U, then S linearly independent. linearly independent.arrow_forward
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

