This is an ordinary differential equation question. Please help with both (a) and (b) Document1 - Microsoft Word (Product Activation Failed)WFileHomeInsertPage LayoutReferencesMailingsReviewView% CutA Find -- A A=,三,“ 请 TAalAaBbCcDc AaBbCcD AaBbC AaBbCc AaBI AqBbCcl1 No Spaci. Heading 1 Heading 2Calibri (Body) - 11AaE Copya ReplacePasteIU- abe x, x*abAI NormalChangeStyles - Select -TitleSubtitleFormat Painter6.ClipboardFontParagraphStylesEditing2:1:1:1 1::2:1·3:1:4:15.16.17:18.1 9.1 10. 1 11. 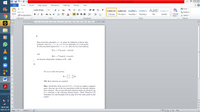| 12.1 13.1 14:1 15: 1 17: 1 18:(a)Show from first principles, i.e., by using the definition of linear inde-pendence, that if u = x+ iy, y +0 is an eigenvalue of a real matrixA with associated eigenvector v = u+ iw, then the two real solutionsY(t) = ea" (u cos bt – w sin bt)andZ(t) = e" (usin bt + w cos bt)are linearly independent solutions of X = AX.(b)Use (a) to solve the systemX = ( :)3X.-8WNB: Real solutions are required.Hint: Recall that if the roots of C(A) = 0 occur in complex conjugateparts, then any one of the two eigenvalues yields two linearly indepen-dent solutions. The second will yield solutions which are identical (upto a constant) to the solutions already found. Check Theorem 2.19(Equation 2.2) and Example 2.20 on page 32 of the study guide in thisregard.ll06:53 AM2022-03-24 Page: 1 of 1 Words: 3B A eE E = 709%+

Answered: Image /qna-images/answer/966093d3-f52e-417b-bc18-bfdbb9bab19e.jpg

Show from first principles, Le., by using the definition of linear inde- pendence, that if µ = z + iy, y # 0 is an eigenvalue of a real matrix A with associated eigenvector e=u+ iw, then the two real solutions Y() = "(u cos dt – w sin be) and Z(1) = e“(usin de + w cos be) are linearly independent solutions of X = AX. (b) Use (a) to solve the system x - (; )x. NB: Real solutions are required. Hint: Recall that if the roots of C(A) = 0 occur in complex conjugate parts, then any one of the two eigenvalues yields two linearly indepen- dent solutions. The second will yleld solutions which are identical (up to a constant) to the solutions already found. Check Theorem 2.19 (Equation 2.2) and Example 2.20 on page 32 of the study guide in this regard.

Show from first principles, Le., by using the definition of linear inde- pendence, that if µ = z + iy, y # 0 is an eigenvalue of a real matrix A with associated eigenvector e=u+ iw, then the two real solutions Y() = "(u cos dt – w sin be) and Z(1) = e“(usin de + w cos be) are linearly independent solutions of X = AX. (b) Use (a) to solve the system x - (; )x. NB: Real solutions are required. Hint: Recall that if the roots of C(A) = 0 occur in complex conjugate parts, then any one of the two eigenvalues yields two linearly indepen- dent solutions. The second will yleld solutions which are identical (up to a constant) to the solutions already found. Check Theorem 2.19 (Equation 2.2) and Example 2.20 on page 32 of the study guide in this regard.

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Similar questions

Please explain how to solve both, thank you!
Please solve differential equation A - By = dy/dx A and B are constant.
please show work
Please explain how to solve thank you!
Please explain how to solve, thank you!