Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Related questions
Question
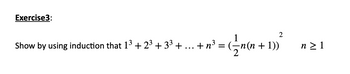
Transcribed Image Text:Exercise3:
Show by using induction that 13 +2³+3³ +
2
+ n³ = ({_n(n + 1))
n≥ 1
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 3 steps
Knowledge Booster
Similar questions
- Can you please explain to me why is (k(k+1) ) / 2 is an integer and I know it always even so can you help me prove that?arrow_forwardFind all sollutions in integers of 34x+8y=6arrow_forwardQ3: What expression can you arrive at when evaluating P(n+1) for the induction step? n+1 A₁-()*+G) •)*+G) <¹-6)* 1- B C 1 [Select] Q4: What expression do you start with for the right hand side of P(n+1)? n (-)" = (₁-1) ²+¹ A n+1 [Select] n+1 B 1- D1- - n 1\n+2 n+2 -(-²) +² D1- n+1 - (²1) ²+¹ E 1-arrow_forward
- 1. Define 0! = 1. For any positive integer n, define n! = n. (n-1)!. For example, 6! = 6 x 5 x 4 x 3×2×1=720. 4" Use induction to show that (2n)! for all integern> 2. (n!)2 n+1arrow_forward2n Using the expansion of (1 + x)²" and given that 211 ²nC₁ + 2(²¹C₂) + 3(²¹℃3) + + 2n(²nC2n) = n × 2²m Show that 1 2(²¹C₁) + 3(²¹C₂) + 4(²¹C3) + + (2n + 1)(²nC₂n) = (n + 1) × 2²narrow_forwardUse the to show that P5(x) = (63x5 – 70x³ + 15x) if given recurrence formula P3(x) = (5x – 3x) and P2(x) =;(3x? – 1). Hence, express P"5(x) in the form of E, Ak Pr(x), as a series of Legendre polynomials.arrow_forward
- Q2(a) For which positive integers n is 3n + 4 < 2"? Prove the inequality using mathematical induction.arrow_forwardCan someone please help me with this? ASAP??!!!arrow_forward"For all integers n, n(n? – 1) is divisible by 6." (You may use quotient-remainder theorem and consider cases.) (You should show your work.)arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY 
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,