Calculus: Early Transcendentals
Calculus: Early Transcendentals
8th Edition
ISBN: 9781285741550
Author: James Stewart
Publisher: Cengage Learning
Bartleby Related Questions Icon

Related questions

Q: mathematical induction
A:
Q: Show that 7 divides 29(52k) + 17(25k-2) for any integer k ≥ 1.
A:
Q: 32. Prove that 3 divides n³ +2n whenever n is a positive integer.
A:
Q: Prove by the method of Mathematical Induction that, 3 divides n3 + 2n for any positive integer n.
A:
Q: Prove 3 | 17k+1-2*5k+3+11k+3 for k>=0 (nonnegative integer)
A: Here in this problem we have to prove that for k≥0 i.e k is a non negative integer…
Q: Use induction to prove that the product of any three consecutive positive integers is divisible by…
A:
Q: Use mathematical induction to prove 1+ 2+ 22 · · ·+ 2n = 2n+1−1 for each integer n ≥ 0
A:
Q: k+4 n(3n +7) k(k +1)(k + 2) 2(n+1)(n+2) k=1
A: Given ∑k=1nk+4k(k+1)(k+2) To show  ∑k=1nk+4k(k+1)(k+2)=n(3n+7)2(n+1)(n+2)
Q: How do I prove that 4 divides 32n-1+1 with induction? (n is natural numbers)
A:
Q: (1) As usual, let (a, b) stand for the Greatest Common Divisor of a and b. Is it true that k(a, b) =…
A:
Q: 2n+1+(-1)" Prove that for all integers n 2 0, 3.2"
A:
Q: Prove by cases For any integer n, n^2 + 5 is not divisible
A:
Q: Prove the claim that there are no integers j and k such that j^2 + 3k^2 = 8
A: Since both j and k are being squared so if we prove the case for positive integers, that will prove…
Q: 5) Let n be a positive integer such that 7 | (8-1). Prove that 7 | (8=*1 - 1). (Hint: Rewrite 8*1…
A: Given: Let n be a positive integer such that 78n-1. To prove: 78n+1-1
Q: Show using induction that 5 divides 8n − 3n for all integers n ≥ 0.
A: Let P(n) be the statement for all integers n greater than equal to 0 Then, 8n-3n is divisible by 5
Q: Prove that 6">5" + 9 for any integer n ≥ 2.
A: Mathematical induction is a technique used to prove statements about well-ordered sets of natural…
Q: 7. For n ≥ 1, verify that 12+32 +52 ++ (2n- +3²+5² · + 2n-1)² = (2n+1) 3
A: Ans : page 1:Ans page 2:
Q: 9. 10. What is t divisors?
A:
Q: For every integer n23 I+ 2+ 2?+ +4^= 4(4n-16) %3D 3. Proof (by induction)
A:
Q: Show that n! > 3ª for n > 7.
A: The given inequality is, n!>3n We need to prove that, the inequality is true for n≥7 Firstly,…
Q: Show that 1+5+9+...+ (4n-3) = 2n²n using mathematical. induction.
A: Base case:    For n = 1:          LHS = 1          RHS = 2.12 - 1 = 2 - 1 = 1      So, LHS = RHS.…
Question
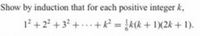
Show by induction that for each positive integer k, 1²+2² + 3² + . … . + k² = }k(k + 1)(2k + 1).
expand button
Transcribed Image Text:Show by induction that for each positive integer k, 1²+2² + 3² + . … . + k² = }k(k + 1)(2k + 1).
Expert Solution
Check Mark
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
See solutionCheck out a sample Q&A here
Step 1
VIEW
Step 2
VIEW
Step 3
VIEW
bartleby

Step by stepSolved in 3 steps with 24 images

See solution
Check out a sample Q&A here
Blurred answer
Knowledge Booster
Background pattern image
Similar questions
Recommended textbooks for you
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Text book image
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Text book image
Precalculus
Calculus
ISBN:9780135189405
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
SEE MORE TEXTBOOKS