
Calculus: Early Transcendentals
8th Edition
ISBN: 9781285741550
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Question
Select the graph which satisfies all of the given conditions.
Show/Explain how you arrived at your answer.

Transcribed Image Text:**Select the graph which satisfies all of the given conditions.**
- \( f'(-3) = f'(2) = 0 \)
- Increasing on \((-3, 2) \cup (2, \infty)\)
- Decreasing on \((-\infty, -3)\)
- \( f''\left(-\frac{4}{3}\right) = f''(2) = 0 \)
- Concave upward on \((-\infty, -\frac{4}{3}) \cup (2, \infty)\)
- Concave downward on \(\left(-\frac{4}{3}, 2\right)\)
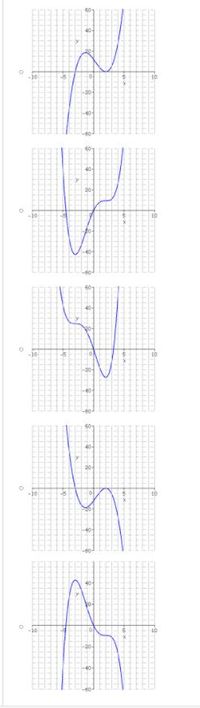
Transcribed Image Text:The image contains five graphs displaying different polynomial functions. Each graph has the following characteristics:
1. **Graph 1:**
- The curve starts below the x-axis, moves above it, and then sharply descends.
- It then rises again, displaying a local maximum.
- Finally, the graph curves upwards steeply, crossing the x-axis.
- The y-axis is labeled from -60 to 60, and the x-axis centers at 0.
2. **Graph 2:**
- The curve shows a similar initial dip and peak as Graph 1, but then it has a higher rising curve.
- This time, there is another dip, before rising into a steep incline.
- The axes are similarly scaled to the first graph.
3. **Graph 3:**
- The curve begins with a downward slope, crosses the x-axis, and peaks before descending sharply.
- After reaching a local minimum, it climbs again and crosses the x-axis.
- This graph has a focus on a balance between positive and negative y-axis values.
4. **Graph 4:**
- It has a steep initial decline to a local minimum, followed by a small peak and then another decline.
- There is another rise afterwards.
- The graph fluctuates above and below the x-axis, covering both positive and negative values.
5. **Graph 5:**
- The pattern starts with a steep initial rise, reaching a local maximum.
- It follows with a steep descent dipping below the x-axis, and then another rise.
- The function displays a tight set of fluctuating values, crossing the x-axis multiple times.
Overall, each graph represents a distinct polynomial function, characterized by varying degrees and behavior of curves. They highlight concepts such as local maxima and minima, inflection points, and x-axis intersections which are critical in understanding polynomial behavior.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 3 images

Knowledge Booster
Similar questions
- Where does the graph of fx equal 3e^x-x/2 have a horizontal positionarrow_forwardfind the intervals where the function is increasing and the interval is decreasing f(x) = 1/3x^3 - 5x^2 + 25x +27arrow_forwardThe revenue (in billions of dollars) from artificial intelligence for enterprise applications in a country for the years from 2016 through 2027 can be modeled by y = 0.872x'./62 where x is the number of years after 2015. (a) Graph the function for the years from 2015 through 2032. (b) Is the function increasing or decreasing over this period of time? (c) Is the graph concave up or down? (d) What is the revenue in 2035?arrow_forward
- Consider the graph of f(x)=4^x. Which of the following shows the related graph h(x)=4^(4+x) ? B What is the horizontal asymptote of f(x)? y = 0 What is the domain of f(x)? (-inf, inf) What is the range of f(x)? (0,inf) What is the y-intercept of f(x)? NEED help here, please What is the horizontal asymptote of h(x)? y = 0 What is the domain of h(x)? help (-inf, inf) What is the range of h(x)? help (0, inf) What is the y-intercept of h(x)? NEED help here, please.arrow_forwardFind f`(x). f`(x)=(8x^2-5x+2)/(x)arrow_forwardThe graph f(x)=3^x is reflected across the cacos shifted downward 5 units and the. Shifted left 2 units. Let g(x) represent the new function. What is an equation for this function? G(x) =? What is the y-intercept of g(x) enter as ordered pair. What is the domain of g(x)? Enter as interval. What is the range of g(x) enter as interval.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning

Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning