Question
See attached graphs
A helicopter takes off from the roof of a building that is 200 feet above the ground. The altitude of the helicopter increases by 150 feet each minute.
(a) Use a formula to express the altitude of a helicopter as a function of time. (Let t be the time in minutes since takeoff and A the altitude in feet.)
A =
(b) Express using functional notation the altitude of the helicopter 90 seconds after takeoff.
A( )
Calculate that value. (Round your answer to the nearest foot.)
ft
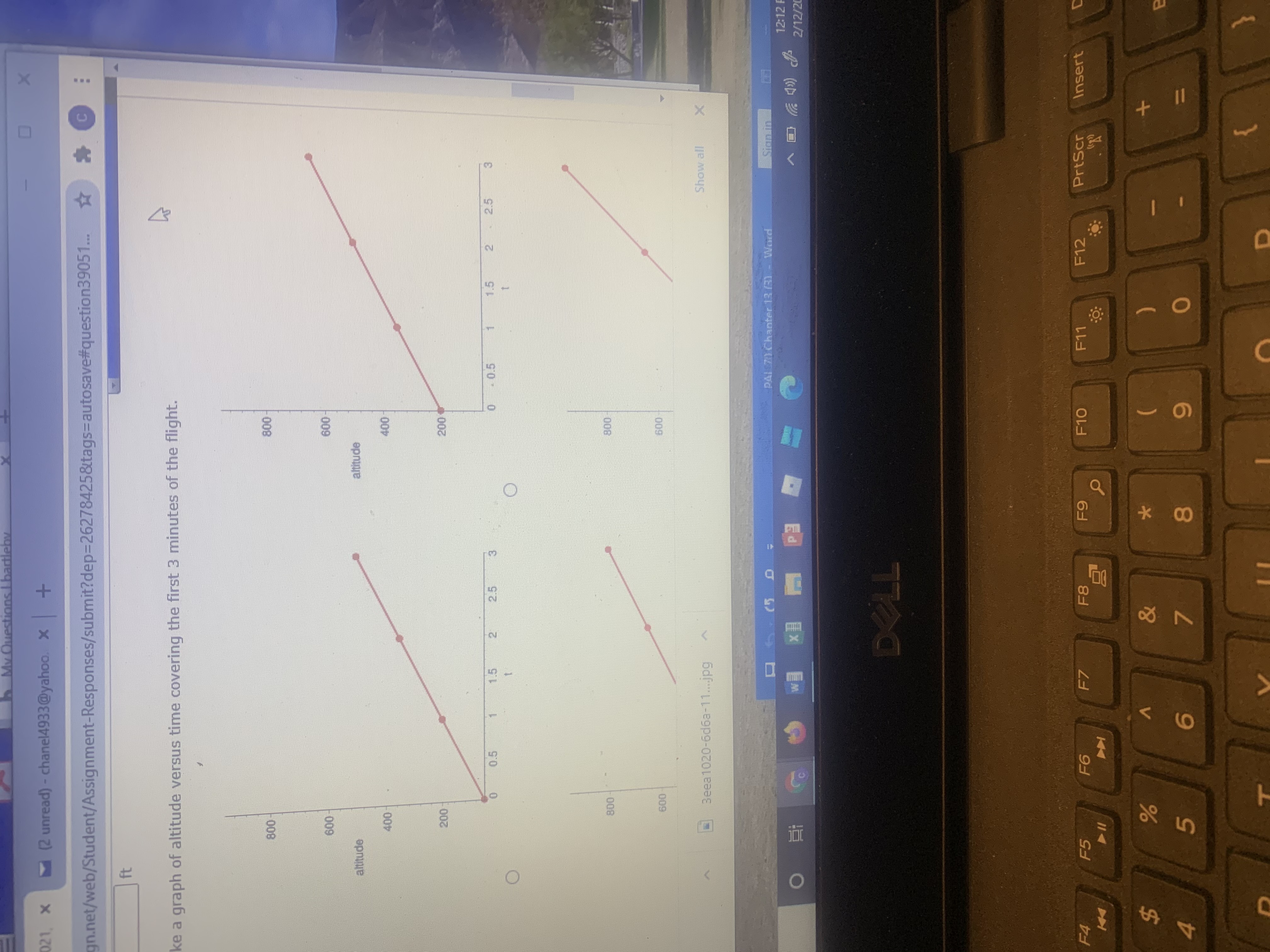
(c) Make a graph of altitude versus time covering the first 3 minutes of the flight.
Explain how the description of the function is reflected in the shape of the graph.
A =
A( )
Calculate that value. (Round your answer to the nearest foot.)
ft
(c) Make a graph of altitude versus time covering the first 3 minutes of the flight.
Explain how the description of the function is reflected in the shape of the graph.
| The altitude changes at a constant rate, and this is reflected in the fact that the graph is a straight line. |
| The altitude decreases at an increasing rate, and this is reflected in the fact that the graph is concave up. |
| The altitude increases at a decreasing rate, and this is reflected in the fact that the graph is concave down. |
| The altitude does not change, and this is reflected in the fact that the graph is a straight line. |
Expert Solution
arrow_forward
Step 1
(a)Initially helicopter is at the height of 200 feet
Altitude of the helicopter increases by 150 feet each minute
Let is the number of minutes since the helicopter take off
Altitude=initial height+number of minutes after take off *rate of increase in amplitude
Hence the height of helicopter minutes after its takeoff is
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 1 images

Knowledge Booster
Similar questions
- A furlong is a distance of 220 yards. A fortnight is a time period of 2 weeks. A race horse is running at a speed of 2.3 yards per second. What is his speed in furlongs per fortnight?.5arrow_forwardHow does something that operates in milliseconds compare to something that operates in nanoseconds? What is the difference in terms of the order of magnitude?arrow_forwardIn the following calculations, be sure to express the answer in standard scientific notation with the appropriate number of significant figures. 3.78 x < 107 g – 4.701 × 105 g - x 10 garrow_forward
- Suppose a machine is invented to measure the amount of knowledge in a student’s head in units called “factoids.” One student is measured at F(t) = t³ − 6t² + 9t factoids at time t, where t is measured in weeks. a. Find the rate at which the student is gaining (or losing) knowledge as a function of time (be sure to give the units). b. During what time between t = 0 and 11 is the student losing knowledge? c. Sketch a graph of the function F(t).arrow_forwardA person's height is approximately 5 feet 2 inches. Express this height in the following terms. (a) meters m (b) centimeters cmarrow_forwardThe bus drops you off at the corner of H Street and 1st Street, approximately 300 ft. from school. You plan to walk to your friend Janneth's house school to work on a project. Approximately how many feet will you have to walk from school to Janneth's house?arrow_forward
arrow_back_ios
arrow_forward_ios