Introductory Circuit Analysis (13th Edition)
13th Edition
ISBN: 9780133923605
Author: Robert L. Boylestad
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Related questions
Question
This is a part of a review I'm studying, NOT a graded assignment, please do not reject. Thank you!
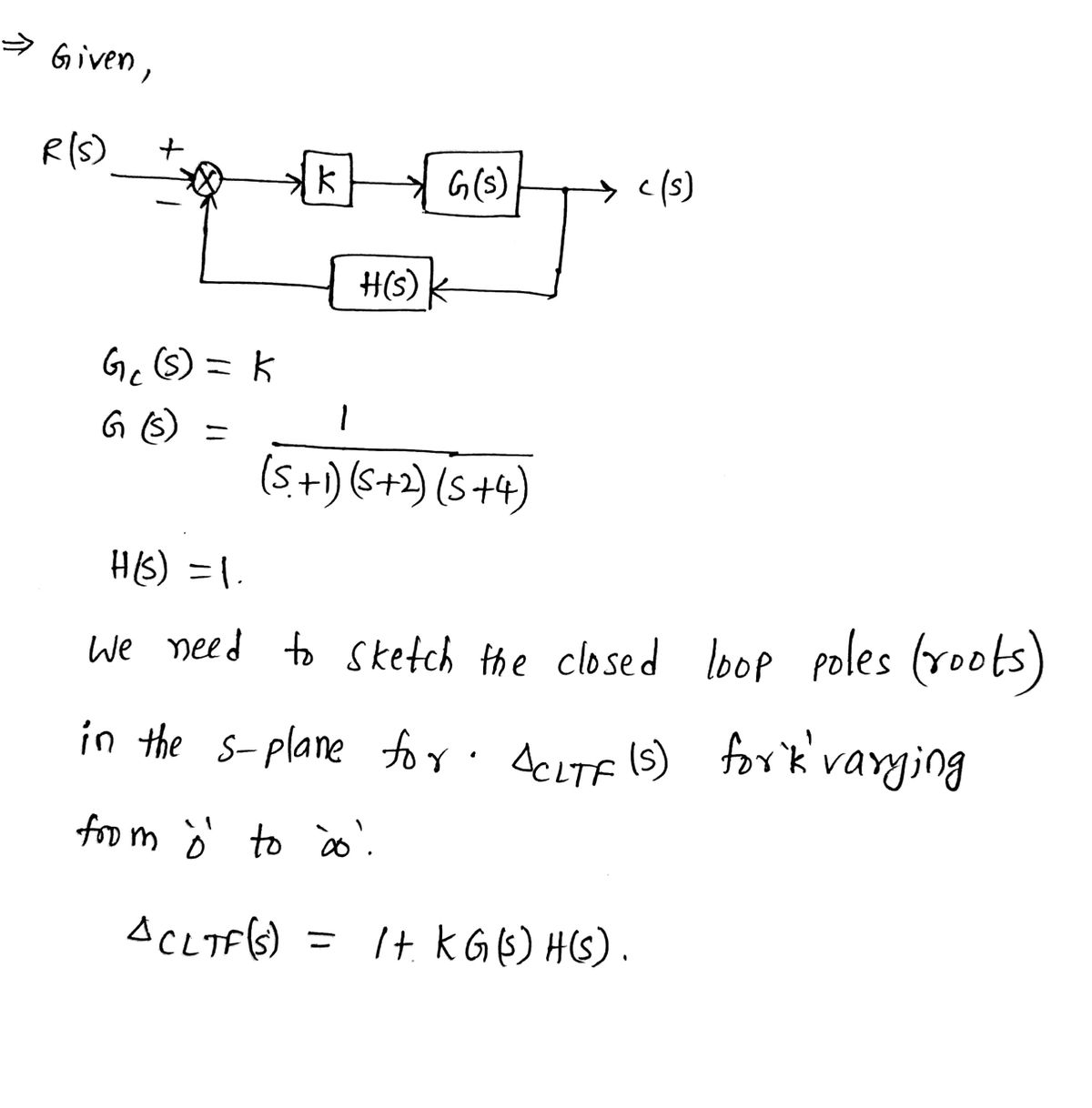
![**Second-order System Performance in Feedback Systems**
---
**Diagram Explanation:**
The diagram displays a block diagram of a feedback system. It consists of the following components:
- **R(s):** Input to the system.
- **K:** Gain block.
- **G(s):** Forward path transfer function.
- **H(s):** Feedback path transfer function.
- **C(s):** Output of the system, with a feedback loop from C(s) to the summing point before K.
The mathematical expression shows the transfer function for the closed-loop system:
\[ C(s) = \left[\frac{KG(s)}{1 + KG(s)H(s)}\right] R(s) \]
The gain \( K \) ranges from \( 0 \leq K < \infty \).
The characteristic equation is given by:
\[ \Delta_{CLTF}(s) = 1 + KG(s)H(s) \]
---
**Example:**
**Objective:** Sketch all the Closed Loop Roots in the S-Plane for \(\Delta_{CLTF}(s)\) for K varying from Zero to Infinite.
---
- **\( G_c(s) = K \):** Controller gain.
- **\( G(s) = \frac{1}{(s+1)(s+2)(s+4)} \):** Transfer function of the plant.
- **\( H(s) = 1 \):** Feedback transfer function.
The closed-loop transfer function is:
\[ T(s) = \frac{KG(s)}{1 + KG(s)H(s)} \]
The characteristic equation remains:
\[ \Delta_{CLTF}(s) = 1 + KG(s)H(s) \]
---
This exercise involves analyzing the roots of the characteristic equation as the gain \( K \) varies from zero to infinity, which is essential for understanding system stability and performance characteristics in control systems.](https://content.bartleby.com/qna-images/question/ecd9d238-92a1-4a47-af9e-c758e887edd1/67b49093-ffd8-48cd-b359-d6c8c8e56df3/xcm98rp_processed.png)
Transcribed Image Text:**Second-order System Performance in Feedback Systems**
---
**Diagram Explanation:**
The diagram displays a block diagram of a feedback system. It consists of the following components:
- **R(s):** Input to the system.
- **K:** Gain block.
- **G(s):** Forward path transfer function.
- **H(s):** Feedback path transfer function.
- **C(s):** Output of the system, with a feedback loop from C(s) to the summing point before K.
The mathematical expression shows the transfer function for the closed-loop system:
\[ C(s) = \left[\frac{KG(s)}{1 + KG(s)H(s)}\right] R(s) \]
The gain \( K \) ranges from \( 0 \leq K < \infty \).
The characteristic equation is given by:
\[ \Delta_{CLTF}(s) = 1 + KG(s)H(s) \]
---
**Example:**
**Objective:** Sketch all the Closed Loop Roots in the S-Plane for \(\Delta_{CLTF}(s)\) for K varying from Zero to Infinite.
---
- **\( G_c(s) = K \):** Controller gain.
- **\( G(s) = \frac{1}{(s+1)(s+2)(s+4)} \):** Transfer function of the plant.
- **\( H(s) = 1 \):** Feedback transfer function.
The closed-loop transfer function is:
\[ T(s) = \frac{KG(s)}{1 + KG(s)H(s)} \]
The characteristic equation remains:
\[ \Delta_{CLTF}(s) = 1 + KG(s)H(s) \]
---
This exercise involves analyzing the roots of the characteristic equation as the gain \( K \) varies from zero to infinity, which is essential for understanding system stability and performance characteristics in control systems.
Expert Solution
arrow_forward
Step 1: State the given data.
Step by stepSolved in 7 steps with 7 images
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, electrical-engineering and related others by exploring similar questions and additional content below.Similar questions
- energyguide labels are not required for TV's, ranges, ovens, and clothes dryers. Why do you think this is true?arrow_forwardSeries Circuit 4.(4) Location Voltage AIA2 Double-click to hide white space BIB2 - Lamp B Cic2 -- Lamp C Across Power Supply - (Entire Circuit) 5.(4a) How does the voltage across the lamps compare?. 6.(4b) How does the voltage of each lamp compare with the voltage of the power supply2 Describe how the voltage changes2 7.(6) Inited States) Focus MacBook Air 88 DII F3 F4 F5 F6 F7 F8 F9 F10 $ 4 6. 7 8. R T. Y U F G H Jarrow_forward
Recommended textbooks for you
- Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON
Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education 
Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education
Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON
Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,
Introductory Circuit Analysis (13th Edition)
Electrical Engineering
ISBN:9780133923605
Author:Robert L. Boylestad
Publisher:PEARSON
Delmar's Standard Textbook Of Electricity
Electrical Engineering
ISBN:9781337900348
Author:Stephen L. Herman
Publisher:Cengage Learning
Programmable Logic Controllers
Electrical Engineering
ISBN:9780073373843
Author:Frank D. Petruzella
Publisher:McGraw-Hill Education
Fundamentals of Electric Circuits
Electrical Engineering
ISBN:9780078028229
Author:Charles K Alexander, Matthew Sadiku
Publisher:McGraw-Hill Education
Electric Circuits. (11th Edition)
Electrical Engineering
ISBN:9780134746968
Author:James W. Nilsson, Susan Riedel
Publisher:PEARSON
Engineering Electromagnetics
Electrical Engineering
ISBN:9780078028151
Author:Hayt, William H. (william Hart), Jr, BUCK, John A.
Publisher:Mcgraw-hill Education,