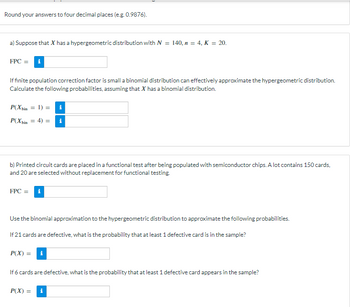
Round your answers to four decimal places (e.g. 0.9876). a) Suppose that X has a hypergeometric distribution with N = 140, n = 4, K = 20. FPC = 1 If finite population correction factor is small a binomial distribution can effectively approximate the hypergeometric distribution. Calculate the following probabilities, assuming that X has a binomial distribution. P(Xbin = 1) = i P(Xbin = = 4) = b) Printed circuit cards are placed in a functional test after being populated with semiconductor chips. A lot contains 150 cards, and 20 are selected without replacement for functional testing. FPC = i Use the binomial approximation to the hypergeometric distribution to approximate the following probabilities. If 21 cards are defective, what is the probability that at least 1 defective card is in the sample? P(X) = If 6 cards are defective, what is the probability that at least 1 defective card appears in the sample? P(X) =

A Poisson distribution with  λ =7.4 λ =7.4 and x=5Use the probability distribution identified above to calculate the following:

Assume that we have two normal distributions both with means 0 and standard deviations σ1 and σ2. If σ1 ≥ σ2, then which of P (0 ≤ x ≤ σ1) and P (0 ≤ x ≤ σ2) is bigger? Explain your answer.

Assume the random variable X is normally distributed with mean μ=50 and standard deviation σ=7. Compute the probability. Be sure to draw a normal curve with the area corresponding to the probability shaded.   P(X>36)     Which of the following normal curves corresponds to P(X>36)​?     A.                 36 50         A normal curve has a horizontal axis with two labeled coordinates, 36 and 50. The curve's peak is near the top of the graph at horizontal coordinate 50. Two vertical line segments run from the horizontal axis to the curve at horizontal coordinates 36 and 50. The area under the curve between the vertical line segments is shaded.   B.                 36 50         A normal curve has a horizontal axis with two labeled coordinates, 36 and 50. The curve's peak is near the top of the graph at horizontal coordinate 50. Two vertical line segments run from the horizontal axis to the curve at horizontal coordinates 36 and 50. The area…