
MATLAB: An Introduction with Applications
6th Edition
ISBN: 9781119256830
Author: Amos Gilat
Publisher: John Wiley & Sons Inc
expand_more
expand_more
format_list_bulleted
Question
thumb_up100%
Round off z-values to two decimal places. Express probabilities in 4 decimal places as found in the provided z-table (Table 1 The Standard Normal.) Include a leading zero before the decimal point, e.g. "0.9999" and not ".9999".
The average waiting time to be seated for dinner at a popular restaurant is 23.2 minutes, with a standard deviation of 3.1 minutes. Assume the variable is normally distributed.
When a customer arrives at the restaurant for dinner, answer the following questions:
Find the probability that the customer will have to wait between 15.5 and 21 minutes:
What is the Probability that the customer will have to wait between 15.5 and 21 min?
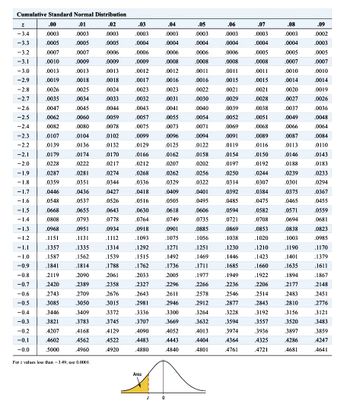
Transcribed Image Text:Cumulative Standard Normal Distribution
Z
.00
.01
.02
.03
.04
.05
.06
.07
.08
.09
-3.4
.0003
.0003
.0003
.0003
.0003
.0003
.0003
.0003
.0003
.0002
-3.3
.0005
.0005
.0005
.0004
.0004
.0004
.0004
.0004
.0004
.0003
-3.2
.0007
.0007
.0006
.0006
.0006
.0006
.0006
.0005
.0005
.0005
-3.1
.0010
.0009
.0009
.0009
.0008
.0008
.0008
.0008
.0007
.0007
-3.0
.0013
.0013
.0013
.0012
.0012
.0011
.0011
.0011
.0010
.0010
-2.9
.0019
.0018
.0018
.0017
.0016
.0016
.0015
.0015
.0014
.0014
-2.8
.0026
.0025
.0024
.0023
.0023
.0022
.0021
.0021
.0020
.0019
-2.7
.0035
.0034
.0033
.0032
.0031
.0030
.0029
.0028
.0027
.0026
-2.6
.0047
.0045
.0044
.0043
.0041
.0040
.0039
.0038
.0037
.0036
-2.5
.0062
.0060
.0059
.0057
.0055
.0054
.0052
.0051
.0049
.0048
-2.4
.0082
.0080
.0078
.0075
.0073
.0071
.0069
.0068
.0066
.0064
-2.3
.0107
.0104
.0102
.0099
.0096
.0094
.0091
.0089
.0087
.0084
-2.2
.0139
.0136
.0132
.0129
.0125
.0122
.0119
.0116
.0113
.0110
-2.1
.0179
.0174
.0170
.0166
.0162
.0158
.0154
.0150
.0146
.0143
-2.0
.0228
.0222
.0217
.0212
.0207
.0202
.0197
.0192
.0188
.0183
-1.9
.0287
.0281
.0274
.0268
.0262
.0256
.0250
.0244
.0239
.0233
-1.8
.0359
.0351
.0344
.0336
.0329
.0322
.0314
.0307
.0301
.0294
-1.7
.0446
.0436
.0427
.0418
.0409
.0401
.0392
.0384
.0375
.0367
-1.6
.0548
.0537
.0526
.0516
.0505
.0495
.0485
.0475
.0465
.0455
-1.5
.0668
.0655
.0643
.0630
.0618
.0606
.0594
.0582
.0571
.0559
-1.4
.0808
.0793
.0778
.0764
.0749
.0735
.0721
.0708
.0694
.0681
-1.3
.0968
.0951
.0934
.0918
.0901
.0885
.0869
.0853
.0838
.0823
-1.2
.1151
.1131
.1112
.1093
.1075
.1056
.1038
.1020
.1003
.0985
-1.1
.1357
.1335
.1314
.1292
.1271
.1251
.1230
.1210
.1190
.1170
-1.0
.1587
.1562
.1539
.1515
.1492
.1469
.1446
.1423
.1401
.1379
-0.9
.1841
.1814
.1788
.1762
.1736
.1711
.1685
.1660
.1635
.1611
-0.8
.2119
.2090
.2061
.2033
.2005
.1977
.1949
.1922
.1894
.1867
-0.7
.2420
.2389
.2358
.2327
.2296
.2266
.2236
.2206
.2177
.2148
-0.6
.2743
.2709
.2676
.2643
.2611
.2578
.2546
.2514
.2483
.2451
-0.5
.3085
.3050
.3015
.2981
.2946
.2912
.2877
.2843
.2810
.2776
-0.4
.3446
.3409
.3372
.3336
.3300
.3264
.3228
.3192
.3156
.3121
-0.3
.3821
.3783
.3745
.3707
.3669
.3632
.3594
.3557
.3520
.3483
-0.2
.4207
.4168
.4129
.4090
.4052
.4013
.3974
.3936
.3897
.3859
-0.1
.4602
.4562
.4522
.4483
.4443
.4404
.4364
.4325
.4286
.4247
-0.0
.5000
.4960
.4920
.4880
.4840
.4801
.4761
.4721
.4681
.4641
For z values less than -3.49, use 0.0001.
Area
Z
0
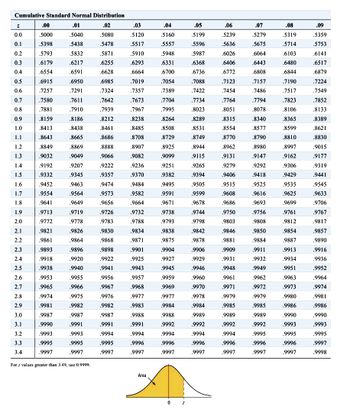
Transcribed Image Text:Cumulative Standard Normal Distribution
Z
.00
.01
.02
.03
.04
.05
.06
.07
.08
.09
0.0
.5000
.5040
.5080
.5120
.5160
.5199
.5239
.5279
.5319
.5359
0.1
.5398
.5438
.5478
.5517
.5557
.5596
.5636
.5675
.5714
.5753
0.2
.5793
.5832
.5871
.5910
.5948
.5987
.6026
.6064
.6103
.6141
0.3
.6179
.6217
.6255
.6293
.6331
.6368
.6406
.6443
.6480
.6517
0.4
.6554
.6591
.6628
.6664
.6700
.6736
.6772
.6808
.6844
.6879
0.5
.6915
.6950
.6985
.7019
.7054
.7088
.7123
.7157
.7190
.7224
0.6
.7257
.7291
.7324
.7357
.7389
.7422
.7454
.7486
.7517
.7549
0.7
.7580
.7611
.7642
.7673
.7704
.7734
.7764
.7794
.7823
.7852
0.8
.7881
.7910
.7939
.7967
.7995
.8023
.8051
.8078
.8106
.8133
0.9
.8159
.8186
.8212
.8238
.8264
.8289
.8315
.8340
.8365
.8389
1.0
.8413
.8438
.8461
.8485
.8508
.8531
.8554
.8577
.8599
.8621
1.1
.8643
.8665
.8686
.8708
.8729
.8749
.8770
.8790
.8810
.8830
1.2
.8849
.8869
.8888
.8907
.8925
.8944
.8962
.8980
.8997
.9015
1.3
.9032
.9049
.9066
.9082
.9099
.9115
.9131
.9147
.9162
.9177
1.4
.9192
.9207
.9222
.9236
.9251
.9265
.9279
.9292
.9306
.9319
1.5
.9332
.9345
.9357
.9370
.9382
.9394
.9406
.9418
.9429
.9441
1.6
.9452
.9463
.9474
.9484
.9495
.9505
.9515
.9525
.9535
.9545
1.7
.9554
.9564
.9573
.9582
.9591
.9599
.9608
.9616
.9625
.9633
1.8
.9641
.9649
.9656
.9664
.9671
.9678
.9686
.9693
.9699
.9706
1.9
.9713
.9719
.9726
.9732
.9738
.9744
.9750
.9756
.9761
.9767
2.0
.9772
.9778
.9783
.9788
.9793
.9798
.9803
.9808
.9812
.9817
2.1
.9821
.9826
.9830
.9834
.9838
.9842
.9846
.9850
.9854
.9857
2.2
.9861
.9864
.9868
.9871
.9875
.9878
.9881
.9884
.9887
.9890
2.3
.9893
.9896
.9898
.9901
.9904
.9906
.9909
.9911
.9913
.9916
2.4
.9918
.9920
.9922
.9925
.9927
.9929
.9931
.9932
.9934
.9936
2.5
.9938
.9940
.9941
.9943
.9945
.9946
.9948
.9949
.9951
.9952
2.6
.9953
.9955
.9956
.9957
.9959
.9960
.9961
.9962
.9963
.9964
2.7
.9965
.9966
.9967
.9968
.9969
.9970
.9971
.9972
.9973
.9974
2.8
.9974
.9975
.9976
.9977
.9977
.9978
.9979
.9979
.9980
.9981
2.9
.9981
.9982
.9982
.9983
.9984
.9984
.9985
.9985
.9986
.9986
3.0
.9987
.9987
.9987
.9988
.9988
.9989
.9989
.9989
.9990
.9990
3.1
.9990
.9991
.9991
.9991
.9992
.9992
.9992
.9992
.9993
.9993
3.2
.9993
.9993
.9994
.9994
.9994
.9994
.9994
.9995
.9995
.9995
3.3
.9995
.9995
.9995
.9996
.9996
.9996
.9996
.9996
.9996
.9997
3.4
.9997
.9997
.9997
.9997
.9997
.9997
.9997
.9997
.9997
.9998
For values greater than 3.49, use 0.9999.
Area
0
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 4 steps with 4 images

Knowledge Booster
Similar questions
- Assume that adults have IQ scores that are normally distributed with a mean of μ=100 and a standard deviation σ=20. Find the probability that a randomly selected adult has an IQ less than 132. The probability that a randomly selected adult has an IQ less than 132 isarrow_forwardA normal distribution has mean u= 56 and standard deviation o = 20. Find and interpret the z-score forx=59. The z-score for x = 59 is So 59 is standard deviations (Choose one) v the mean u = 56.arrow_forwardAssume that adults have IQ scores that are normally distributed with mean of mu = 100 and a standard deviation sigma=20, Find the probability that a randomly selected adult has an IQ 80 and 120 the probability that a randomly selected adult has an IQ between 80 and 120 is (type an integer or decimal rounfed to four decimal places as needed)arrow_forward
- Assume that adults have IQ scores that are normally distributed with a mean of mμ=100 and a standard deviation σ= 15. Find the probability that a randomly selected adult has an IQ less than 127. The probability that a randomly selected adult has an IQ less tha 127 isarrow_forwardAssume that adults have IQ scores that are normally distributed with a mean of μ=105 and a standard deviation σ=20. Find the probability that a randomly selected adult has an IQ between 93 and 117.arrow_forwardPlz help ASAParrow_forward
- Suppose that the TSH (Thyroid Stimulating Hormone) levels among healthy individuals are normally distributed with a mean of 3.3 unitsmL. Suppose also that exactly 95% of healthy individuals have TSH levels below 6.2 unitsmL. Find the standard deviation of the distribution of TSH levels of healthy individuals. Carry your intermediate computations to at least four decimal places. Round your answer to at least two decimal places.arrow_forwardAssume that adults have IQ scores that are normally distributed with a mean of µ = 100 and a standard deviation o = 20. Find the probability that a randomly selected adult has an IQ between 80 and 120.arrow_forwardSuppose that the distance of fly balls hit to the outfield (in baseball) is normally distributed with a mean of 236 feet and a standard deviation of 44 feet. We randomly sample 49 fly balls. Part (a) If X =average distance in feet for 49 fly balls, then give the distribution of X. Round your standard deviation to two decimal places. X ____, ________,_______ ~ . Part (b) What is the probability that the 49 balls traveled an average of less than 226 feet? (Round your answer to four decimal places.)Sketch the graph. Scale the horizontal axis for X. Shade the region corresponding to the probability. Part (c) Find the 70th percentile of the distribution of the average of 49 fly balls. (Round your answer to two decimal places.) ft †arrow_forward
- On average, indoor cats live to 14 years old with a standard deviation of 2.7 years. Suppose that the distribution is normal. Let X = the age at death of a randomly selected indoor cat. Round answers to 4 decimal places where possible.A. The middle 50% of indoor cats' age of death lies between what two numbers? Low: years High: yearsarrow_forwardAssume that adults have IQ scores that are normally distributed with a mean of μ=105 and a standard deviation σ=15. Find the probability that a randomly selected adult has an IQ less than 123.arrow_forwardAssume that adults have 1Q scores that are normally distributed with a mean of 103.1 and a standard deviation of 24.4. Find the probability that a randomly selected adult has an IQ greater than 131.3. (Hint: Drawa graph.) The probability that a randomly selected adult from this group has an IQ greater than 131.3 is (Round to four decimal places as needed.)arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman

MATLAB: An Introduction with Applications
Statistics
ISBN:9781119256830
Author:Amos Gilat
Publisher:John Wiley & Sons Inc

Probability and Statistics for Engineering and th...
Statistics
ISBN:9781305251809
Author:Jay L. Devore
Publisher:Cengage Learning

Statistics for The Behavioral Sciences (MindTap C...
Statistics
ISBN:9781305504912
Author:Frederick J Gravetter, Larry B. Wallnau
Publisher:Cengage Learning

Elementary Statistics: Picturing the World (7th E...
Statistics
ISBN:9780134683416
Author:Ron Larson, Betsy Farber
Publisher:PEARSON

The Basic Practice of Statistics
Statistics
ISBN:9781319042578
Author:David S. Moore, William I. Notz, Michael A. Fligner
Publisher:W. H. Freeman

Introduction to the Practice of Statistics
Statistics
ISBN:9781319013387
Author:David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:W. H. Freeman