Roulette is a casino game that involves players betting on where a ball will land on a spinning wheel. An American roulette wheel has 38 numbered slots — half of the slots from 1 to 36 are red and the other half are black. Slots 00 and 00 are both green. Suppose that a player bets $1 on a single slot. If the ball lands in their slot, the player gets their initial $1 back plus a payout of $35. If the ball doesn't land in their slot, they lose their $1 bet. Let X= the player's net gain from a $1 bet on a single slot. Here is the probability distribution of X: Find the expected value of a player's net gain on a $1 bet on a single slot. You may round your answer to the nearest thousandth

Roulette is a casino game that involves players betting on where a ball will land on a spinning wheel. An American roulette wheel has 38 numbered slots — half of the slots from 1 to 36 are red and the other half are black. Slots 00 and 00 are both green. Suppose that a player bets $1 on a single slot. If the ball lands in their slot, the player gets their initial $1 back plus a payout of $35. If the ball doesn't land in their slot, they lose their $1 bet. Let X= the player's net gain from a $1 bet on a single slot. Here is the probability distribution of X: Find the expected value of a player's net gain on a $1 bet on a single slot. You may round your answer to the nearest thousandth

Name: Roulette is a casino game that involves players betting on where a bal
Uploaded: 2024-03-20T07:06:41.000Z
Channel: Bartleby
Description: Roulette is a casino game that involves players betting on where a ball will land on a spinning wheel. An American roulette wheel has 38 numbered slots — half of the slots from 1 to 36 are red and the other half are black. Slots 00 and 00 are both gr

A First Course in Probability (10th Edition)

10th Edition

ISBN:9780134753119

Author:Sheldon Ross

Publisher:Sheldon Ross

Chapter1: Combinatorial Analysis

Section: Chapter Questions

Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...

See similar textbooks

Related questions

Q: In roulettem, if a player uses the doubling strategy starting with a $10 bet and is betting on red…

A: Given that, Odds are one-one

Q: A game involves tossing two coins and receiving 70¢ if they are both heads. What is a fair price to…

A: When we toss two coins the sample space is S={HH,HT,TH,TT} n(S)=4 Let E be the event of getting both…

Q: Suppose you are invited to play a game in which you bet $1 on any number from 000 to 599. If your…

A: Given that there are numbers from 000 and 599. That is, there are 600 numbers. If your number comes…

Q: If the famous insurance company, Brendan's of Jacksonville, insures a $3 million Monet painting for…

A: In the given case there are two possibilities The claim will arrive if painting gets stolen and the…

Q: (a) Find the expected value of playing the game. dollars (b) What can Alonzo expect in…

Q: 2. Suppose you're on the Las Vegas strip, and an enthusiastic stranger approaches you asking if…

A: a. For a valid probability distribution, P(X=x) ≥ 0 and Σ P(X=x) = 1

Q: A certain game involves tossing 3 fair coins, and it pays 20¢ for 3 heads, 9¢ for 2 heads, and 5¢…

A: Given data A certain game involves tossing 3 fair coins it pays 20c for 3 heads , 9c for 2 heads ,…

Q: (A) Create a payoff table for 0, 1, 2, and 3 winning tickets among the 5 tickets you purchased. (If…

A: Given,the pay-off values of the tickets.To create a payoff table and calculate it's expected value…

Q: Suppose you play a game where you toss three fair coins. If you get three tails, you win $10.…

A: Probability of getting a tail while tossing a coin is 1/2 So, if 3 coins will be tossed then the…

Q: A certain game involves tossing 3 fair coins, and it pays 18¢ for 3 heads, 9¢ for 2 heads, and 3¢…

A: Given A certain game involves tossing 3 fair coins, and it pays 18¢ for 3 heads, 9¢ for 2 heads, and…

Q: A slot machine has three dials. Each dial has 30 positions, one of which is jackpot. To win the…

A: Given information- We have given that a slot machine has three dials. Each dial has 30 positions,…

Q: at a casino, you throw a fair 4 sided dice whose sides are labeled 1, 2, 3 and 4. If you land on…

A: Solution: Total number of sides in a fair dice is = 4 Sides labeled as = 1, 2, 3, 4 The…

Q: ou are on a TV show. You have been asked to either play a dice game five times or accept a $150…

A: Expectation of a Random Variable: The expectation of a random variable X, denoted by E(X), is…

Q: What expectation does a person with $15 have who bets on heads, be- ginning with a $1 bet, and uses…

A: The bettor has $15 with him and start bet with $1 as well as uses doubling technique. He plays four…

Q: Dr. Neel asks you if you would like to play a game of chance. He has a jar filled with 100 marbles.…

A: Total marbles, n= 100 Probability of selecting Blue marble= probability of earn 1 point= P(B)=…

Q: Kaitlin has a bag with 8 balls numbered 1 through 8. She is playing a game of chance. This game is…

Q: The chance of winning Florida's Pick-6 Lotto game is 1 in approximately 23 million. Suppose you buy…

A: Random variables are of 2 types, discrete and continuous. A discrete random variable can only take…

Q: Heather is playing a game of chance in which she rolls a number cube with sides numbered from 1 to…

A: Given Loses value=2.75

Q: Find the expected value of the psychic's profit by filling in the boxes below with you answers. Use…

A: Reviewing information, PBoy=0.51P(Girl)=0.49Cost=$20If psychic is wrong, he has to pay back $20

Q: Your friend offers to place a bet with you. He will pay you$1if your favorite sports team wins the…

A: Let X be the random variable denoting the amount of money ($) you win or lose. And P(X) denotes the…

Q: Suppose you decided to play a gambling game. In order to play the game there is a $1.00 dollar fee…

A: Given that xx P(x)P(x) (you roll a 1, 2, 3) (you roll a 1, 2, 3) (you roll a 4 or 5) (you…

Q: The world famous gambler from Philadelphia, Senior Rick, proposes the following game of chance. You…

Q: quarter lands o him $1 0 bo wi:1

A: consider two coins c and c' suppose c is a special two headed coin and c' is a standard coin having…

Q: Suppose you are invited to play a game in which you bet $1 on any number from 000 to 599. If your…

A: Number from 000 and 599 If your number comes up you get $300 We have to find Expected wining

Q: In the casino game of American roulette, the wheel is divided into 38 compartments numbered 1…

A: Given Information: There are 38 compartments numbered 1 through 36, 0, and 00. One-half of the…

Q: Which of the following games involving the roll of a single die is a fair bet A. Bet $1 and receive…

A: The question revolves around determining which of the given bets involving the roll of a single die…

Q: n the gambling game "craps", a pair of dice is rolled and the outcome of the experiment is the sum…

A: (a) List the sample space for the pair of the dice. The sample space for the pair of the dice is…

Q: How much should you win or lose if any other number turns up in order for the game to be fair?

A: Here two dice are rolled So Total possible outcomes 6× 6 = 36

Q: Reuben is playing a game of chance in which he rolls a number cube with sides numbered from 1 to 6.…

A: Given that - Reuben is playing a game of chance in which he rolls a number cube with sides numbered…

Q: you roll two standard dice. If you roll doubles, then you pay $5. If the game is fair, what would…

A: You are rolling 2 standard dice which means both these dices have 6 faces each. That means that…

Q: What did the insurance company charge Charlie for this policy if the company expected to break even?

A: Here given Charlie buys a one-year term home insurance policy for $p, that will pay $200,000 in the…

Q: the carnival has come to town, and lucky louie has once again set up his pavilion. He offers a…

A: Given two normal six sided dice are rolledtotal number of possibilities when two dice are rolled =…

Concept explainers

Contingency Table

A contingency table can be defined as the visual representation of the relationship between two or more categorical variables that can be evaluated and registered. It is a categorical version of the scatterplot, which is used to investigate the linear relationship between two variables. A contingency table is indeed a type of frequency distribution table that displays two variables at the same time.

Binomial Distribution

Binomial is an algebraic expression of the sum or the difference of two terms. Before knowing about binomial distribution, we must know about the binomial theorem.

Topic Video

Question

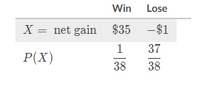
Suppose that a player bets $1 on a single slot. If the ball lands in their slot, the player gets their initial $1 back plus a payout of $35. If the ball doesn't land in their slot, they lose their $1 bet. Let X= the player's net gain from a $1 bet on a single slot. Here is the probability distribution of X:

Find the expected value of a player's net gain on a $1 bet on a single slot.
You may round your answer to the nearest thousandth.

Win
Lose
X = net gain $35
-$1
1
37
P(X)
38
38

Video Video

Expert Solution

This question has been solved!

Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.

This is a popular solution!

SEE SOLUTION Check out a sample Q&A here

Step 1

VIEW

Step 2

VIEW

Trending now

This is a popular solution!

Step by step

Solved in 2 steps

SEE SOLUTION Check out a sample Q&A here

Knowledge Booster

$Discrete Probability Distributions$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, probability and related others by exploring similar questions and additional content below.

Similar questions

After giving the lotto a try you decide to go back to Clayton Campus for some more gambling action. Theyare playing a die tossing game where you win a brand new home if you roll all sides of the die within 7rolls. Your crystal ball can see into the future and tells you that when you roll the die 7 times you don't seethe same number appear twice in a row. You decide to bet your entire rent for the year and try to win thehouse. You toss a fair six-sided die 7 times. Consider the following events, A = “each value appears atleast once” and B = “the outcome is alternate in numbers (i.e., a specific face of the die cannot be observed to occur directly after it was observed on the previous roll but it may have occurred elsewhere inthe sequence of rolls)”. What is p(A|B)? Are you likely to win the house?
You draw a card from a deck of 52 cards. If the card is a spade, you win $5, but if the card is not a spade you lose $2.What is your expected earning from this game?
A pair of fair dice is rolled onoe, Suppose that you lose $7 if the dice sum to 5 and win $8 if the dice sum to 11 or 12. How much should you win or lose if any other number tums up in order for the game to be fair? To keep the game fair, you should (Do not round until the final answer. Then round to the nearest cent as needed.) if the dice sum to any other number
If I $6 to play a spinner game and the chances of winning $1 dollar is 50% and the chances of winning $12 is 50%. What is the fair price of the game?
There is a game of chance called "Lightning Dice" at a charity carnival. It costs $2 to play. The player then rolls 4 dice. If the player rolls 3 or more sixes, then the player wins $30. Otherwise, the player wins nothing. How much can you expect to gain or lose if you play this game 68 times?
A friend proposes a gamble to you. You roll 2 fair, six-sided dice, and add up the results of each die to find your total number. If your roll totals a 6 or 8, your friend pays you $30. If you roll any other total, you pay your friend $10. What is your expected payoff from playing this game 100 times?.
a pair of dice is rolled once. Suppose that you lose 9$ if the dice sum to 5 and win 10$ if the dice sum to 11 or 8. How much should you win or lose if any other number turns up in order for the game to be fair?
The St. Petersburg paradox is a coin flip game, where a fair coin is tossed successively, until heads occurs. If the first toss is heads, you win $1. If the first one is tails and the second one is heads, you win $2. If the first heads occurs in the third toss, you win $4 and so forth. The amount of money you win is doubled with each coin flip you survive. In the eighteenth century it was believed that the fair price for participating in such a game would be the expected wealth you gain. Show that the expectation value of the St. Petersburg game is infinite.
James placed a $25 bet on a red and a $5 bet on the number 33 (which is black) on a standard 00 roulette wheel. -if the ball lands in a red space, he wins $25 on his 'red' but loses $5 on his '33' bet - so he wins $20 -if the ball lands the number 33, he loses $25 on his 'red' bet but wins $175 on his '33' bet: He wins $150 -if the ball lands on a spae that isn't red and isnt 33 he loses both bets, so he loses $30 So for each spin; he either wins $150, wins $20, or loses $30 -probability that he wins $150 is 1/38 or .0263 -probability that he wins $20 is 18/38 or .4737 -probability that he loses $30 is 19/38 or .5000 let X = the profit that james makes on the next spin x P (X=x) x*P(X=x) x^2*P(X=x) 150 .0263 3.945 591.75 20 .4737 9.474 189.48 -30 .5000 -15.000 450.00 sum (sigma) 1.000 -1.581 1231.23 u (expected value)= -$1.581 variance = 1228.73044 standard deviation = 35.053 FILL IN THE BLANK if you play 2500 times, and Let, x (x bar)= the mean winnings (or…
One option in a roulette game is to bet $7 on red. (There are 18 red compartments, 18 black compartments, and two compartments that are neither red nor black.) If the ball lands on red, you get to keep the $7 you paid to play the game and you are awarded $7. If the ball lands elsewhere, you are awarded nothing and the $7 that you bet is collected. Complete parts (a) through (b) below. III a. What is the expected value for playing roulette if you bet $7 on red? $ (Round to the nearest cent.) b. What does this expected value mean? Choose the correct statement below. O A. This value represents the expected loss over the long run for each game played. OB. Over the long run, the player can exper to break even. OC. This value represents the expected win over the long run for each game played.
A certain game involves tossing 3 fair coins, and it pays 11¢ for 3 heads, 7¢ for 2 heads, and 4e for 1 head. Is 7¢a fair price to pay to play this game? That is, does the 7¢ cost to play make the game fair? .... The 7¢ cost to play a fair price to pay because the expected winnings are (Type an integer or a fraction. Simplify your answer.)