
MATLAB: An Introduction with Applications
6th Edition
ISBN: 9781119256830
Author: Amos Gilat
Publisher: John Wiley & Sons Inc
expand_more
expand_more
format_list_bulleted
Question
Pls answer the wrong ones clearly.
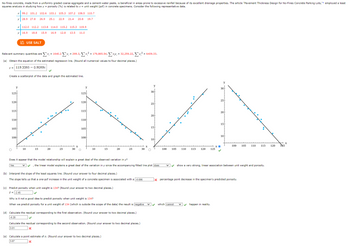
Transcribed Image Text:No-fines concrete, made from a uniformly graded coarse aggregate and a cement-water paste, is beneficial in areas prone to excessive rainfall because of its excellent drainage properties. The article "Pavement Thickness Design for No-Fines Concrete Parking Lots,"+ employed a least
squares analysis in studying how y = porosity (%) is related to x = unit weight (pcf) in concrete specimens. Consider the following representative data.
Relevant summary quantities are Σxi = 1640.2 ΣΥ; = 299,3, Σx? = 179,865,54, Σ×y; = 32,259,22, Σy = 6409.33.
(a) Obtain the equation of the estimated regression line. (Round all numerical values to four decimal places.)
119.3385 -0.9089x
125
Create a scatterplot of the data and graph the estimated line.
120
y
115
110
x 99.2 101.2 102.6
103.1 105.3 107.2 108.5 110.7
y 28.9 27.8 26.9 25.1 22.9 21.4 20.8 19.7
105
x 112.0 112.2 113.8 114.0 115.2 115.3
119.9
y 16.9 18.8 15.9 16.9 12.8 13.5 11.0
100
O
USE SALT
10
15
20
25
30
y
125
120
115
110
105
100
O
10
15
20
(c) Predict porosity when unit weight is 134? (Round your answer to two decimal places.)
ŷ = -2.45
25
(b) Interpret the slope of the least squares line. (Round your answer to four decimal places.)
The slope tells us that a one-pcf increase in the unit weight of a concrete specimen is associated with a -0.696
(e) Calculate a point estimate of a. (Round your answer to two decimal places.)
3.87
X
30
(d) Calculate the residual corresponding to the first observation. (Round your answer to two decimal places.)
-0.28
Calculate the residual corresponding to the second observation. (Round your answer to two decimal places.)
3.01
x
y
30
Does it appear that the model relationship will explain
great deal of the observed variation in y?
Yes
✓✓ the linear model explains a great deal of the variation in y since the accompanying fitted line plot does
25
20
15
10
Why is it not a good idea to predict porosity when unit weight is 134?
When we predict porosity for a unit weight of 134 (which is outside the scope of the data) the result is negative ✓ ✓
100 105 110
which cannot
y
30
25
✔✔✔happen in reality.
20
15
XO
125
120
10
Xpercentage point decrease in the specimen's predicted porosity.
100 105 110
show a very strong, linear association between unit weight and porosity.
115
120
125
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 3 images

Knowledge Booster
Similar questions
Recommended textbooks for you
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman

MATLAB: An Introduction with Applications
Statistics
ISBN:9781119256830
Author:Amos Gilat
Publisher:John Wiley & Sons Inc

Probability and Statistics for Engineering and th...
Statistics
ISBN:9781305251809
Author:Jay L. Devore
Publisher:Cengage Learning

Statistics for The Behavioral Sciences (MindTap C...
Statistics
ISBN:9781305504912
Author:Frederick J Gravetter, Larry B. Wallnau
Publisher:Cengage Learning

Elementary Statistics: Picturing the World (7th E...
Statistics
ISBN:9780134683416
Author:Ron Larson, Betsy Farber
Publisher:PEARSON

The Basic Practice of Statistics
Statistics
ISBN:9781319042578
Author:David S. Moore, William I. Notz, Michael A. Fligner
Publisher:W. H. Freeman

Introduction to the Practice of Statistics
Statistics
ISBN:9781319013387
Author:David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:W. H. Freeman