A First Course in Probability (10th Edition)
10th Edition
ISBN: 9780134753119
Author: Sheldon Ross
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Related questions
Question
Give the answer
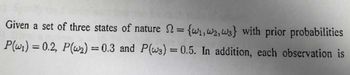
Transcribed Image Text:Given a set of three states of nature \( \Omega = \{\omega_1, \omega_2, \omega_3\} \) with prior probabilities \( P(\omega_1) = 0.2 \), \( P(\omega_2) = 0.3 \), and \( P(\omega_3) = 0.5 \). In addition, each observation is
![The image contains a problem related to Gaussian class-conditional probability density functions and decision-making in the context of machine learning or statistical classification. Here is the transcription and description as if it were for an educational website:
---
In the context of a decision-making problem, we consider a scalar \( x \) with Gaussian class-conditional probability density functions (pdf) expressed as \( p(x \mid \omega_i) \sim \mathcal{N}(\mu_i, \sigma_i^2) \) for \( 1 \leq i \leq 3 \). Specifically, the parameters of the distributions are given as:
\[
\mu_1 = -1, \quad \mu_2 = 0, \quad \mu_3 = 2
\]
\[
\sigma_1 = 2, \quad \sigma_2 = 1, \quad \sigma_3 = 3
\]
Please address the following questions:
a) In the case of minimum-error-rate classification, which state of nature should we decide for \( x = 1.5 \)?
b) Suppose we have a set of two possible actions \( A = \{\alpha_1, \alpha_2\} \) with the following loss function:
| Class | \(\omega = \omega_1\) | \(\omega = \omega_2\) | \(\omega = \omega_3\) |
|-------|------------------|------------------|------------------|
| \(\alpha = \alpha_1\) | 5 | 10 | 20 |
| \(\alpha = \alpha_2\) | 10 | 30 | 3 |
For an observation \( x \) with value 0.5, which action should we apply on \( x \)?
---
This problem illustrates decision theory concepts using Gaussian distributions to model the likelihood of different classes and a loss matrix to evaluate decision-making actions based on observed data.](https://content.bartleby.com/qna-images/question/5d860cd5-2859-4da0-be1a-b0f5f49f917c/4cd26135-511d-4384-81d7-d16e6bfa29d9/wi098sb_processed.jpeg)
Transcribed Image Text:The image contains a problem related to Gaussian class-conditional probability density functions and decision-making in the context of machine learning or statistical classification. Here is the transcription and description as if it were for an educational website:
---
In the context of a decision-making problem, we consider a scalar \( x \) with Gaussian class-conditional probability density functions (pdf) expressed as \( p(x \mid \omega_i) \sim \mathcal{N}(\mu_i, \sigma_i^2) \) for \( 1 \leq i \leq 3 \). Specifically, the parameters of the distributions are given as:
\[
\mu_1 = -1, \quad \mu_2 = 0, \quad \mu_3 = 2
\]
\[
\sigma_1 = 2, \quad \sigma_2 = 1, \quad \sigma_3 = 3
\]
Please address the following questions:
a) In the case of minimum-error-rate classification, which state of nature should we decide for \( x = 1.5 \)?
b) Suppose we have a set of two possible actions \( A = \{\alpha_1, \alpha_2\} \) with the following loss function:
| Class | \(\omega = \omega_1\) | \(\omega = \omega_2\) | \(\omega = \omega_3\) |
|-------|------------------|------------------|------------------|
| \(\alpha = \alpha_1\) | 5 | 10 | 20 |
| \(\alpha = \alpha_2\) | 10 | 30 | 3 |
For an observation \( x \) with value 0.5, which action should we apply on \( x \)?
---
This problem illustrates decision theory concepts using Gaussian distributions to model the likelihood of different classes and a loss matrix to evaluate decision-making actions based on observed data.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Step 1: Write the given information.
VIEW Step 2: Determine the state of nature to be decided for x = 1.5.
VIEW Step 3: Compute the posterior probabilities P(wi | x=0.50) for w1, w2 and w3 using Bayes' theorem.
VIEW Step 4: Determine the action to be applied on x based on given table.
VIEW Solution
VIEW 
Trending nowThis is a popular solution!
Step by stepSolved in 5 steps with 15 images
Knowledge Booster
Similar questions
- Cynthia is president of an international chemical distribution company, Cchem. Weekly gross sales for Cchem has a mean of $1 million and standard deviation of $0.2 million; the distribution of sales is highly right-skewed. One week’s sales are independent of the sales in any other week. Use this information to answer questions 5 to 6 below. What is the probability that sales for the week of October 5, 2009 will be more than $1.25 million? In order for Cynthia to receive a bonus, Cchem’s annual sales must exceed $53 million. What is the probability that Cynthia will receive a bonus for the fiscal year starting in 2010? Assume there are 52 weeks in a year.arrow_forwardDetermine the values of x, if x² = 324. Select the TWO that apply. and :: x = -18 : x = 18 : x = 162arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- A First Course in Probability (10th Edition)ProbabilityISBN:9780134753119Author:Sheldon RossPublisher:PEARSON
A First Course in Probability (10th Edition)
Probability
ISBN:9780134753119
Author:Sheldon Ross
Publisher:PEARSON