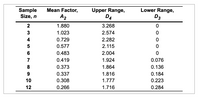
m6hw3#2 The given table provides statistical factors used in quality control processes, specifically control chart computations. The table is structured with rows representing different sample sizes and columns indicating the mean factor and range constants.### Table Summary:- **Sample Size, \(n\)**: It ranges from 2 to 12, indicating the number of observations in a sample.- **Mean Factor, \(A_2\)**: This column lists the values used to calculate the control limits of the average chart when the standard deviation is not known. - For \(n = 2\), \(A_2 = 1.880\) - For \(n = 3\), \(A_2 = 1.023\) - For \(n = 4\), \(A_2 = 0.729\) - For \(n = 5\), \(A_2 = 0.577\) - For \(n = 6\), \(A_2 = 0.483\) - For \(n = 7\), \(A_2 = 0.419\) - For \(n = 8\), \(A_2 = 0.373\) - For \(n = 9\), \(A_2 = 0.337\) - For \(n = 10\), \(A_2 = 0.308\) - For \(n = 12\), \(A_2 = 0.266\)- **Upper Range, \(D_4\)**: Represents the factor used to determine the upper control limit of range charts. - For \(n = 2\), \(D_4 = 3.268\) - For \(n = 3\), \(D_4 = 2.574\) - For \(n = 4\), \(D_4 = 2.282\) - For \(n = 5\), \(D_4 = 2.115\) - For \(n = 6\), \(D_4 = 2.004\) - For \(n = 7\), \(D_4 = 1.924\) - For \(n = 8\), \(D_4 = 1.864\) - For \(n = 9\), \(D_ Refer to Table S6.1 - Factors for Computing Control Chart Limits (3 sigma) for this problem.Thirty-five samples of size 7 each were taken from a fertilizer-bag-filling machine at Panos Kouvelis Lifelong Lawn Ltd. The results were: Overall mean = 60.75 lb.; Average range \( \overline{R} \) = 1.64 lb.a) For the given sample size, the control limits for 3-sigma \( \overline{X} \) chart are:Upper Control Limit (UCL \(_{\overline{X}}\)) = \[\_\_\_\_\_\_\_\] lb. (round your response to three decimal places).

Answered: Image /qna-images/answer/5bdc3f79-164f-4548-8da3-40ebf5d01653.jpg

Refer to Table S6.1 - Factors for Computing Control Chart Limits (3 sigma) for this problem. Thirty-five samples of size 7 each were taken from a fertilizer-bag-filling machine at Panos Kouvelis Lifelong Lawn Ltd. The results were: Overall mean = 60.75 lb.; Average range R = 1.64 Ib. a) For the given sample size, the control limits for 3-sigma x chart are: Upper Control Limit (UCL;) = Ib. (round your response to three decimal places).