
Elementary Geometry For College Students, 7e
7th Edition
ISBN: 9781337614085
Author: Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher: Cengage,
expand_more
expand_more
format_list_bulleted
Question
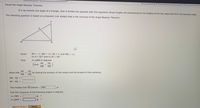
Transcribed Image Text:Recall the Angle-Bisector Theorem.
If a ray bisects one angle of a triangle, then it divides the opposite side into segments whose lengths are proportional to the lengths of the two sides that form the bisected angle.
The following question is based on a theorem (not stated) that is the converse of the Angle-Bisector Theorem.
i
Given:
NP = 12, MN = 18, PQ = 8, and MQ = 12;
%3D
%3D
mzP = 62° and mzM = 36°
Find:
M QNM in degrees
NP
Hint:
PQ
MN
MQ
PQ
NP
Show that
MN
by finding the product of the means and the product of the extremes.
MQ
%3D
MN · PQ
%3D
NP· MQ
%3D
This implies that NQ bisects MNP
Find the measures of the following angles in degrees.
%3D
Need Help?
Read It
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
- in ABCD, lines BH is perpendicular to AD and line BG is perpendicular to CD. How are ABH and CBG related? a- Congruent b- same areas c- similar d- same perimetersarrow_forwardDecide whether the given measurements of the SSA case can form exactly one triangle, exactly two triangles, or no triangle. C = 65º, c = 44, b = 32arrow_forwardIn △ABC, AB = 5, BC = 6, and CA = 7. E and F are points on sides AC and AB, respectively so that AF = 2 and AE = 4. Line FE intersects line BC at point D. What is BD?arrow_forward
- 4. a) A blue jay, B, is sitting atop of an electrical tower as shown. i) Draw and shade in the angle that would represent the angle of depression of the bluejay as it looks down at an ant, A, on the ground. [T = 1] ii) What is the measure of this angle of depression? [T = 1] b) A pigeon, P is also on the tower as shown. Determine the vertical distance between the two birds (i.e. determine the height of line segment BP). Number your steps for clarity. Round to one decimal place, where needed. P- [T = 3] 40° 25° MathBits.com A 87 feetarrow_forwardIn triangle ABC, DE intersects sides AB and AC and is parallel to side BC. If AD = 6; DB = 8; AE = 9; EC = ?arrow_forwardPlease answer the question below, all parts. Thank youarrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning