
College Physics
11th Edition
ISBN: 9781305952300
Author: Raymond A. Serway, Chris Vuille
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
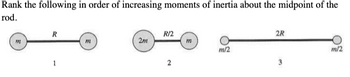
Transcribed Image Text:**Ranking Moments of Inertia**
The task is to rank the following systems in order of increasing moments of inertia about the midpoint of the rod:
1. **Diagram 1:**
- **Masses:** Two identical masses \( m \)
- **Distance:** Each mass is located at a distance \( R \) from the midpoint.
2. **Diagram 2:**
- **Masses:** A mass \( 2m \) and a mass \( m \)
- **Distance:** The mass \( 2m \) is at a distance \( R/2 \) from the midpoint, and the mass \( m \) is at the same distance \( R/2 \) on the opposite side.
3. **Diagram 3:**
- **Masses:** Two identical masses \( m/2 \)
- **Distance:** Each mass is located at a distance \( 2R \) from the midpoint.
**Explanation:**
- **Moment of Inertia (I)** is calculated using the formula \( I = \sum m_i r_i^2 \), where \( m_i \) is the mass and \( r_i \) is the distance from the axis of rotation (midpoint in this case).
For each system:
- **Diagram 1:** Moment of inertia is \( 2mR^2 \).
- **Diagram 2:** Moment of inertia is \( (2m)(R/2)^2 + (m)(R/2)^2 = \frac{3}{2}m \left( \frac{R^2}{4} \right) = \frac{3}{4}mR^2 \).
- **Diagram 3:** Moment of inertia is \( 2 \times (m/2) (2R)^2 = 8mR^2 \).
**Rank:**
2 (Smallest) < 1 < 3 (Largest)
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 5 steps with 3 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- A figure skater performs a twisting jump. She rotates around her longitudinal axis 2 times in 0.65 s. What was her average angular velocity in radians/second? A 720rad/s B 19.3rad/s C 4? rad/s D 9.67 rad/s E 1107 rad/sarrow_forwardThree identical balls, with masses of M, 2M, and 3M, are fastened to a massless rod of length L as shown. Determine the rotational inertia about the right end of the rod. L/2 L/2 3M M O 7ML"2 /2 O ZML"2 /3 O ML"2 O SML"2arrow_forwardIf an object has a moment of inertia 37 kg-m2 and the magnitude of its rotational angular momentum is 88 kg · m2/s, what is its rotational kinetic energy? Krot =arrow_forward
- The three 'point' masses are as shown in the figure. m, = 2.0 kg at (x, y) =(0,0), m₂ = 3.0 kg at (4,3), and m3 = 4.0 kg at (8,0), respectively. What is the moment of inertia of the masses about the y axis? +y=3 m x=4 marrow_forwardQuestion 5 only.......arrow_forwardy 11 P a aa- X If a = 4 in, determine the moment of inertia about the x-axis located at point P.arrow_forward
- A ball of radius Ris rolling across a rough surface without slipping. What is the relationship between the angular speed w and the translational speed v? Image size: Select the correct answer Ου-R/ω Ου- 1/ω O v= w Ου-ω/R O V = Rwarrow_forwardA thin rod of mass m and length 3R connects two spheres of mass m and radius R.Find the moment of inertia of the system about the axis at the midpoint of the rod and perpendicular to it. 3R R R m marrow_forwardA volley ball players 4.4 kg arm moves at an average angular velocity of 16 rad/s during the execution of a spike. if the average moment of inertia of the extending arm is 0.39 kg*m^2. what is the average radius of rotation for the arm during the spike?arrow_forward
- Find the moment of inertia for a uniform rod (mass m and length L) about an axis at the position shown in the figurearrow_forwardge A person 1.93 m tall swings their leg from the hip at 141 degrees/s. Calculate the linear tangential velocity (v) of the end of their leg to 2 decimal places. Answer: to search 7 R E 4 P P Next page FTSE 100arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON

College Physics
Physics
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning

University Physics (14th Edition)
Physics
ISBN:9780133969290
Author:Hugh D. Young, Roger A. Freedman
Publisher:PEARSON

Introduction To Quantum Mechanics
Physics
ISBN:9781107189638
Author:Griffiths, David J., Schroeter, Darrell F.
Publisher:Cambridge University Press

Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning

Lecture- Tutorials for Introductory Astronomy
Physics
ISBN:9780321820464
Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina Brissenden
Publisher:Addison-Wesley

College Physics: A Strategic Approach (4th Editio...
Physics
ISBN:9780134609034
Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart Field
Publisher:PEARSON