Question
Solve ASAP, vll upvote but dont use chatgpt
Transcribed Image Text:Question 3:
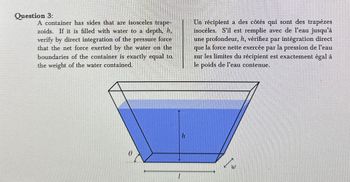
A container has sides that are isosceles trape-
zoids. If it is filled with water to a depth, 1,
verify by direct integration of the pressure force
that the net force exerted by the water on the
boundaries of the container is exactly equal to
the weight of the water contained.
Un récipient a des côtés qui sont des trapèzes
isocèles. S'il est remplie avec de l'eau jusqu'à
une profondeur, h, vérifiez par intégration direct
que la force nette exercée par la pression de l'eau
sur les limites du récipient est exactement égal à
le poids de l'eau contenue.
Ө
h
I
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 1 images

Knowledge Booster
Similar questions
arrow_back_ios
arrow_forward_ios