
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
please answer the following question with the formula listed
![**Question 11:**
Let's try the Gram-Schmidt process of orthogonalization with the matrix:
\[
\begin{bmatrix}
0.223 & 0.668 & 0.710 \\
-0.125 & 0.741 & 0.660 \\
0.795 & -0.234 & 0.560 \\
\end{bmatrix}
\]
What is the y-coordinate of r3-prime? (Don't normalize r3-prime, simply follow the steps, do not use the cross product)
Round your answer to 3 decimal places.
[Answer box]](https://content.bartleby.com/qna-images/question/c8ef3851-b223-4be3-ac39-739e48c0c7a3/b76e1d24-3b15-413b-9bae-42e0844cea36/m53n184_thumbnail.png)
Transcribed Image Text:**Question 11:**
Let's try the Gram-Schmidt process of orthogonalization with the matrix:
\[
\begin{bmatrix}
0.223 & 0.668 & 0.710 \\
-0.125 & 0.741 & 0.660 \\
0.795 & -0.234 & 0.560 \\
\end{bmatrix}
\]
What is the y-coordinate of r3-prime? (Don't normalize r3-prime, simply follow the steps, do not use the cross product)
Round your answer to 3 decimal places.
[Answer box]
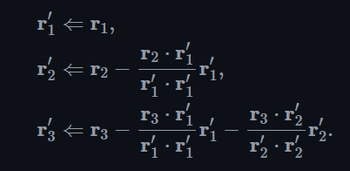
Transcribed Image Text:The text in the image appears to be a series of vector equations used in mathematics, possibly in the context of numerical methods or linear algebra. The equations are as follows:
1. \( \mathbf{r}_1' \gets \mathbf{r}_1 \),
2. \( \mathbf{r}_2' \gets \mathbf{r}_2 - \frac{\mathbf{r}_2 \cdot \mathbf{r}_1'}{\mathbf{r}_1' \cdot \mathbf{r}_1'} \mathbf{r}_1' \),
3. \( \mathbf{r}_3' \gets \mathbf{r}_3 - \frac{\mathbf{r}_3 \cdot \mathbf{r}_1'}{\mathbf{r}_1' \cdot \mathbf{r}_1'} \mathbf{r}_1' - \frac{\mathbf{r}_3 \cdot \mathbf{r}_2'}{\mathbf{r}_2' \cdot \mathbf{r}_2'} \mathbf{r}_2' \).
Explanation:
- These equations appear to describe a process of vector orthogonalization, possibly using the Gram-Schmidt process.
- \( \mathbf{r}_1' \) is initialized as \( \mathbf{r}_1 \).
- \( \mathbf{r}_2' \) is obtained by projecting \( \mathbf{r}_2 \) onto \( \mathbf{r}_1' \) and then subtracting this projection from \( \mathbf{r}_2 \), ensuring \( \mathbf{r}_2' \) is orthogonal to \( \mathbf{r}_1' \).
- \( \mathbf{r}_3' \) is computed similarly by orthogonalizing \( \mathbf{r}_3 \) with respect to both \( \mathbf{r}_1' \) and \( \mathbf{r}_2' \), ensuring it is orthogonal to both.
These steps are fundamental in creating an orthogonal set of vectors from a linearly independent set.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps

Knowledge Booster
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

