Question 1: Case Studies: Applications of Linear Algebraic Equations (Mechanical Engineering) SPRING-MASS SYSTEMS Idealized spring-mass systems have numerous applications throughout engineering. Figure below shows an arrangement of four springs in series being depressed. X₁ 2 xz 5 X₁ ■ I llllllllllll At equilibrium, force-balance equations can be developed defining the interrelationships between the springs. k₂(x₂-x₁) = k₁x₁ k₂ (x₂-x₂)=k₂ (x₂-x k₂(x₂-x₂) = k₂(x₂-x2) F=k_(x₂-x₂) where the K's are spring constants. If k1 through k4 are 100, 50, 80, and 200 N/m, respectively and with a force of 14,700N. www
Question 1: Case Studies: Applications of Linear Algebraic Equations (Mechanical Engineering) SPRING-MASS SYSTEMS Idealized spring-mass systems have numerous applications throughout engineering. Figure below shows an arrangement of four springs in series being depressed. X₁ 2 xz 5 X₁ ■ I llllllllllll At equilibrium, force-balance equations can be developed defining the interrelationships between the springs. k₂(x₂-x₁) = k₁x₁ k₂ (x₂-x₂)=k₂ (x₂-x k₂(x₂-x₂) = k₂(x₂-x2) F=k_(x₂-x₂) where the K's are spring constants. If k1 through k4 are 100, 50, 80, and 200 N/m, respectively and with a force of 14,700N. www
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:Question 1:
Case Studies: Applications of Linear Algebraic Equations (Mechanical Engineering)
SPRING-MASS SYSTEMS
Idealized spring-mass systems have numerous applications throughout engineering.
Figure below shows an arrangement of four springs in series being depressed.
2
H
0
!
llllllllllll
2
Task: Formulate the force-balance equations in matrix Ax=8 form
N
At equilibrium, force-balance equations can be developed defining the interrelationships between the springs,
k₂ (x₂-x₁) = k₁x₁
k₂(x₂-x₂)=k₂ (x₂-x2)
k₂(x₂-x₂) = k₂(x₂-x2)
F=k_(x₂-x₂)
where the K's are spring constants. If k1 through k4 are 100, 50, 80, and 200 N/m, respectively and with a force of 14,700N.

Transcribed Image Text:Task: Formulate the force-balance equations in matrix Ax-B form
A
B
k₂+k₂ −k₂
2
-k₂ k₂-k₂-k 3
0
0
0
2
-k₂ k₂+k₂
3
3
-k₂ k₂+k3 - k3
0
-k₂ k₂+k₁
3
3
k₁+k₂ −k₂
1 2
-k₂ 0
2
0
-k₂
3
0 0
k₁+k₂ −k₂
2
0 0
-k₂ k₂+k₂ −k₂
2
2 3
-k₂
4
-k
0
3
-k
4
k₂+k
3
-K₂ K₂+k₂ - k3
2
2 3
0
k₂+k₁
-k
0
-k₁
4
0 0
3
0
4
-k
k₂+kk
4
-k k
4
4
0 0
4
4
-k
4
X
X
X
X
X
X
X
1
X
3
st
3
x2
1
0
1
H
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 3 steps

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
refer to your answer in question 1
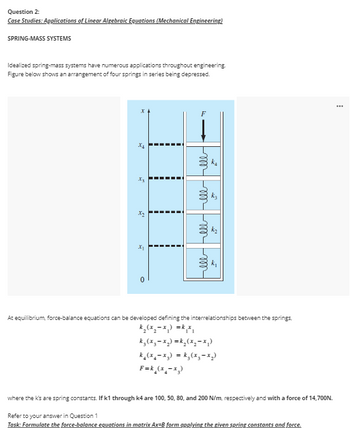
Transcribed Image Text:Question 2:
Case Studies: Applications of Linear Algebraic Equations (Mechanical Engineering)
SPRING-MASS SYSTEMS
Idealized spring-mass systems have numerous applications throughout engineering.
Figure below shows an arrangement of four springs in series being depressed.
X4
W
2
O
I
H
lll lll lll lll
At equilibrium, force-balance equations can be developed defining the interrelationships between the springs,
k₂(x₂-x₁) = k₁x₁
k₂ (x₂-x₂)=k₂(x₂-x₁)
k₂(x₂-x₂) = k₂(x₂-x₂)
F=k_(x₂-x₂)
where the K's are spring constants. If k1 through k4 are 100, 50, 80, and 200 N/m, respectively and with a force of 14,700N.
Refer to your answer in Question 1
Task: Formulate the force-balance equations in matrix Ax-B form applying the given spring constants and force.
***
Solution
Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

