Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
Q7 Fill in the Blank a. This is the arm of the angle that lies along the positive x- axis. b. The digits in a decimal follow a pattern. c. This is when two angles have the same terminal arm. d. The acute angle whose vertex is at the origin and whose arms are the terminal arm of the angle and the x-axis. e. Two perpendicular lines called axis that make four quadrants. f. This is the arm of an angle in standard position that meets the initial arm at the origin to form an angle. g. An angle in standard position whose terminal arr lies on one of the axes. h. This is when an angle's initial arm lies along the positive x- axis, the vertex is located at the origin and the terminal arm lies anywhere in the Cartesian plane. 1. The values are given fraction form. j. The digits in a decimal do not follow a pattern. k. The number of digits in a decimal are finite. 1. The number of digits in a decimal are infinite. Type in your answer. Coterminal angle

Q7 Fill in the Blank a. This is the arm of the angle that lies along the positive x- axis. b. The digits in a decimal follow a pattern. c. This is when two angles have the same terminal arm. d. The acute angle whose vertex is at the origin and whose arms are the terminal arm of the angle and the x-axis. e. Two perpendicular lines called axis that make four quadrants. f. This is the arm of an angle in standard position that meets the initial arm at the origin to form an angle. g. An angle in standard position whose terminal arr lies on one of the axes. h. This is when an angle's initial arm lies along the positive x- axis, the vertex is located at the origin and the terminal arm lies anywhere in the Cartesian plane. 1. The values are given fraction form. j. The digits in a decimal do not follow a pattern. k. The number of digits in a decimal are finite. 1. The number of digits in a decimal are infinite. Type in your answer. Coterminal angle

Algebra & Trigonometry with Analytic Geometry
Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN:9781133382119
Author:Swokowski
Publisher:Swokowski
Chapter6: The Trigonometric Functions
Section6.1: Angles
Problem 3E
See similar textbooks
icon
Related questions
Question

1) The question screenshot attached down below answer question 7,8 and only need final answer.

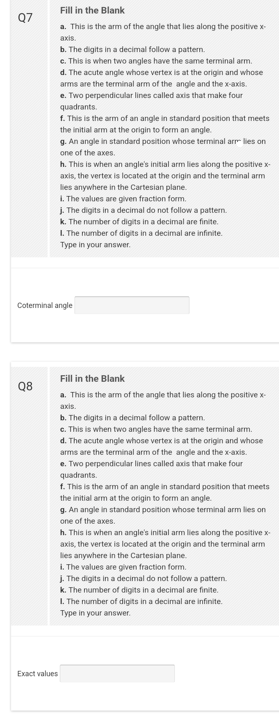
Q7 Q8 Fill in the Blank a. This is the arm of the angle that lies along the positive x- axis. Exact values b. The digits in a decimal follow a pattern. c. This is when two angles have the same terminal arm. d. The acute angle whose vertex is at the origin and whose arms are the terminal arm of the angle and the x-axis. e. Two perpendicular lines called axis that make four quadrants. f. This is the arm of an angle in standard position that meets the initial arm at the origin to form an angle. g. An angle in standard position whose terminal arr lies on one of the axes. Coterminal angle h. This is when an angle's initial arm lies along the positive x- axis, the vertex is located at the origin and the terminal arm lies anywhere in the Cartesian plane. 1. The values are given fraction form. j. The digits in a decimal do not follow a pattern. k. The number of digits in a decimal are finite. 1. The number of digits in a decimal are infinite. Type in your answer. Fill in the Blank a. This is the arm of the angle that lies along the positive x- axis. b. The digits in a decimal follow a pattern. c. This is when two angles have the same terminal arm. d. The acute angle whose vertex is at the origin and whose arms are the terminal arm of the angle and the x-axis. e. Two perpendicular lines called axis that make four quadrants. f. This is the arm of an angle in standard position that meets the initial arm at the origin to form an angle. g. An angle in standard position whose terminal arm lies on one of the axes. h. This is when an angle's initial arm lies along the positive x- axis, the vertex is located at the origin and the terminal arm lies anywhere in the Cartesian plane. i. The values are given fraction form. j. The digits in a decimal do not follow a pattern. k. The number of digits in a decimal are finite. 1. The number of digits in a decimal are infinite. Type in your answer.
Transcribed Image Text:Q7 Q8 Fill in the Blank a. This is the arm of the angle that lies along the positive x- axis. Exact values b. The digits in a decimal follow a pattern. c. This is when two angles have the same terminal arm. d. The acute angle whose vertex is at the origin and whose arms are the terminal arm of the angle and the x-axis. e. Two perpendicular lines called axis that make four quadrants. f. This is the arm of an angle in standard position that meets the initial arm at the origin to form an angle. g. An angle in standard position whose terminal arr lies on one of the axes. Coterminal angle h. This is when an angle's initial arm lies along the positive x- axis, the vertex is located at the origin and the terminal arm lies anywhere in the Cartesian plane. 1. The values are given fraction form. j. The digits in a decimal do not follow a pattern. k. The number of digits in a decimal are finite. 1. The number of digits in a decimal are infinite. Type in your answer. Fill in the Blank a. This is the arm of the angle that lies along the positive x- axis. b. The digits in a decimal follow a pattern. c. This is when two angles have the same terminal arm. d. The acute angle whose vertex is at the origin and whose arms are the terminal arm of the angle and the x-axis. e. Two perpendicular lines called axis that make four quadrants. f. This is the arm of an angle in standard position that meets the initial arm at the origin to form an angle. g. An angle in standard position whose terminal arm lies on one of the axes. h. This is when an angle's initial arm lies along the positive x- axis, the vertex is located at the origin and the terminal arm lies anywhere in the Cartesian plane. i. The values are given fraction form. j. The digits in a decimal do not follow a pattern. k. The number of digits in a decimal are finite. 1. The number of digits in a decimal are infinite. Type in your answer.
Expert Solution
steps

Step by step

Solved in 2 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Algebra & Trigonometry with Analytic Geometry
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage
Algebra: Structure And Method, Book 1
Algebra: Structure And Method, Book 1
Algebra
ISBN:
9780395977224
Author:
Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:
McDougal Littell
Holt Mcdougal Larson Pre-algebra: Student Edition…
Holt Mcdougal Larson Pre-algebra: Student Edition…
Algebra
ISBN:
9780547587776
Author:
HOLT MCDOUGAL
Publisher:
HOLT MCDOUGAL
College Algebra (MindTap Course List)
College Algebra (MindTap Course List)
Algebra
ISBN:
9781305652231
Author:
R. David Gustafson, Jeff Hughes
Publisher:
Cengage Learning
Trigonometry (MindTap Course List)
Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning
Mathematics For Machine Technology
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
SEE MORE TEXTBOOKS