Related questions
Question
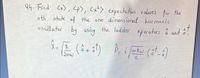
Transcribed Image Text:Q4. Find <x>, <p>, <x?> expectation values for the
nth state of the one dimensional harmenic
oscillator å!.
by using the ladder operatars å and
12mw
2.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 4 steps
Knowledge Booster
Similar questions
- A quantum mechanical particle of mass m moves in a 1D potential where a) Estimate the ground state energy of the particle. b) Sketch the wave function to the best of your ability.arrow_forwardn=2 35 L FIGURE 1.0 1. FIGURE 1.0 shows a particle of mass m moves in x-axis with the following potential: V(x) = { 0, for 0arrow_forwardWhat is the independent wave function for a particle in a box x=0,Larrow_forward
arrow_back_ios
arrow_forward_ios