Q19. A 5-lb ball B is traveling around in a horizontal circle of radius ₁ = 4.6 ft with a speed (VB)₁ = 4.9 ft/s. If the attached cord is pulled down through the hole with a constant speed v₁ = 2.1 ft/s, determine how far is the ball from the hole when the ball reaches a speed of 15 ft/s. Please pay attention: the numbers may change since they are randomized. Your answer must include 2 places after the decimal point, and proper unit. B ri (VB)1 Your Answer: Answer Vr units

Answered: Q19. A 5-lb ball B is traveling around in a horizontal circle of radius ₁ = 4.6 ft with a speed (VB)₁ = 4.9 ft/s. If the attached cord is pulled down through…

Elements Of Electromagnetics

7th Edition

ISBN: 9780190698614

Author: Sadiku, Matthew N. O.

Publisher: Oxford University Press

See similar textbooks

Concept explainers

Conservation of Energy

In physics, the rule of the conservation of energy states that energy doesn’t disappear from the atmosphere; instead, it changes its form from one type to another. Energy is one of the most important physical quantities in nature, and it cannot be create…

Question

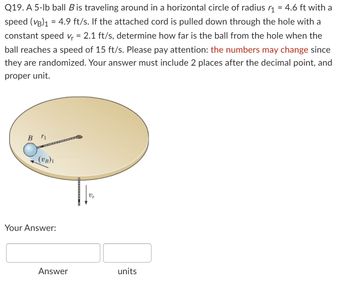
Q19. A 5-lb ball B is traveling around in a horizontal circle of radius r₁ = 4.6 ft with a
speed (VB)₁ = 4.9 ft/s. If the attached cord is pulled down through the hole with a
constant speed v₁ = 2.1 ft/s, determine how far is the ball from the hole when the
ball reaches a speed of 15 ft/s. Please pay attention: the numbers may change since
they are randomized. Your answer must include 2 places after the decimal point, and
proper unit.
B ri
(VB)1
Your Answer:
Answer
Vr
units

Expert Solution

Step 1

To find-:

The final distance of ball from the hole.

Given-:

The weight of the ball is $W = 5 l b$ .

The initial radius of rotation of ball is $r_{1} = 4.61 f t$ .

The initial speed of the ball is ${(V_{B})}_{1} = 4.9 \frac{f t}{s}$ .

The speed of the chord with which it is being pulled is $V_{r} = 2.1 \frac{f t}{s}$ .

The final speed of the ball is $V_{B} = 15 \frac{f t}{s}$ .

FBD-:

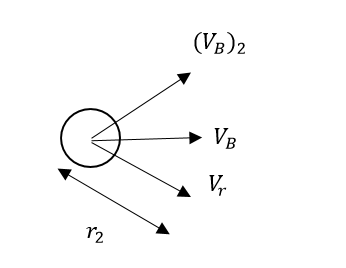
Calculations-:

At given final position, the net velocity of the ball is the resultant of final tangential velocity of ball ${(V_{B})}_{2}$ and velocity of cord $V_{r}$ i.e-:

$\vec{V_{B}} = {(\vec{V_{B}})}_{2} + \vec{V_{r}}$

${(V_{B})}^{2} = {{(V_{B})}_{2}}^{2} + {(V_{r})}^{2}$ (1)

Substitute the value of $V_{B} = 15 \frac{f t}{s}$ and $V_{r} = 2.1 \frac{f t}{s}$ in equation (1).

$\begin{array}{rcl} {(15)}^{2} & = & {{(V_{B})}_{2}}^{2} + {(2.1)}^{2} \\ {{(V_{B})}_{2}}^{2} & = & 225 - 4.41 \\ {(V_{B})}_{2} & = & 14.85 \frac{f t}{s} \end{array}$

Since, there is no external torque, hence angular momentum will remains conserved. So, initial angular momentum is equal to final angular momentum.

$m {(V_{B})}_{1} r_{1} = m {(V_{B})}_{2} r_{2}$

Here, $m$ is the mass of the ball and $r_{2}$ is the final distance of ball from the hole.

${(V_{B})}_{1} r_{1} = {(V_{B})}_{2} r_{2}$ (2)

Substitute the value of ${(V_{B})}_{1} = 4.9 \frac{f t}{s}$ , $r_{1} = 4.61 f t$ and ${(V_{B})}_{2} = 14.85 \frac{f t}{s}$ in equation (2).

$4.9 \times 4.61 = 14.85 \times r_{2} r_{2} = 1.52 f t$

Thus, the final distance of ball from the hole is $r_{2} = 1.52 f t$ .

Step by stepSolved in 2 steps with 1 images

See solution

Check out a sample Q&A here

Knowledge Booster

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.

Related questions

Concept explainers